На этом шаге мы рассмотрим рекурсивную реализацию такой цепи.

    Цель следующей задачи - упростить электрическую цепь на рисунке 1, напоминающую многозвенную схему, содержащую несколько уровней резисторов, сопротивление которых равно r.

Такое соединение называется ещё резисторной схемой лестничного типа или резисторной «лестницей».

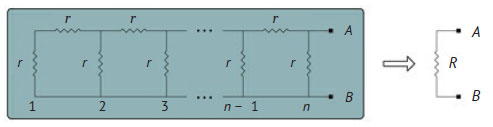
Рис.1. Задача о резистивной цепи

    В частности, можно заменить всю цепь эквивалентной, состоящей из одного резистора.

    Таким образом, задача состоит в определении значения сопротивления R (как функции сопротивления r), приводящего к эквивалентной цепи. На рисунке 2 показано, как преобразовать цепь из двух резисторов с сопротивлениями r₁ и r₂, если они соединены последовательно (a) или параллельно (b).

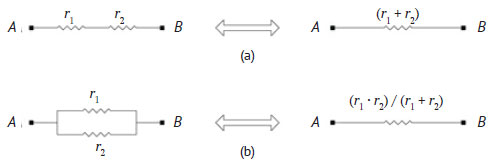
Рис.2. Эквивалентность резисторных соединений

    При последовательном соединении получающееся сопротивление равно r₁ + r₂, а при параллельном новое сопротивление r = (r₁ * r₂)/(r₁ + r₂), или иначе:

    1/r = 1/r1 + 1/r2               (4.6).

    Эти правила можно применять последовательно к парам резисторов, пока не получится цепь из одного резистора. Однако данный процесс утомителен, и вместо него предлагается короткое и изящное рекурсивное решение задачи.

    Задача имеет два входных параметра: сопротивление r и число звеньев n в цепи. Очевидно, размер задачи - n (r влияет на выходное значение задачи (результат), но не влияет на время выполнения алгоритма). Пусть R(r, n) обозначает рекурсивную функцию. Начальное условие выполняется при n = 1, когда начальная цепь состоит только из одного резистора. Значит, в этом случае R(r, 1) = r. Для вывода рекурсивного условия нужно отыскать в исходной задаче подзадачу с точно такой же структурой. Рисунок 3(a) показывает декомпозицию задачи с уменьшением её размера на 1.

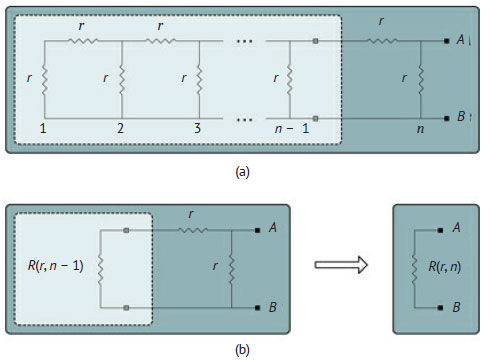
Рис.3. Декомпозиция задачи о резистивной цепи и вывод рекурсивного условия методом индукции

    Цепь, соответствующая подзадаче, может быть заменена единственным резистором с сопротивлением R(r, n - 1), как показано на рисунке 3(b), когда на основании метода индукции можно считать её значение известным. Наконец, легко упростить получающуюся цепь, состоящую всего из трёх резисторов. Во-первых, левый и верхний резисторы соединены последовательно. Значит, их можно объединить в один резистор с сопротивлением R(r, n - 1) + r. Наконец, этот новый резистор соединён параллельно с правым резистором. Применяя (4.6), R(r, n) можно определить как:

    1/R(r, n) = 1/r + 1/(R(r, n - 1) + r).

    Таким образом, рекурсивная функция:

                  r,  если n = 1,
    R(r, n) = 
                 1/(1/r + 1/(R(r, n -1) + r)), если n > 1       .

    В примере 4.17 приведён соответствующий код. И наконец, любопытное замечание: можно показать, что R(r, n) = rF(2n - 1) / F(2n), где F - функция Фибоначчи.

def circuit(n, r):
    if n == 1:
        return r
    else:
        return 1 / (1 / r + 1 / (circuit(n - 1, r) + r))    

    На следующем шаге мы приведем решения нескольких задач.

Предыдущий шаг Содержание Следующий шаг