На этом шаге мы рассмотрим реализацию этой задачи при помощи рекурсии.

Треугольник Паскаля - треугольное представление биномиальных коэффициентов (ⁿ_m), приведённое на рисунке 1, где треугольник (a) содержит сами биномиальные коэффициенты, а треугольник (b) - их фактические целочисленные значения.

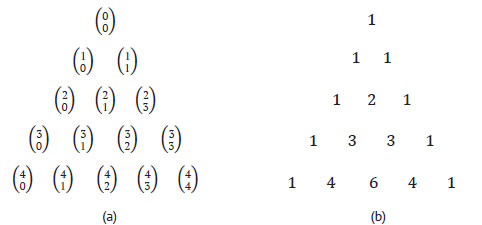
Рис.1. Треугольник Паскаля

Очередная наша задача - определить список биномиальных коэффициентов n-й строки: где первые и последние элементы всегда равны 1. Задачу можно рассмотреть с рекурсивной точки зрения, принимая во внимание определение (3.2). Графически это означает, что биномиальный коэффициент - это сумма пары коэффициентов, расположенных непосредственно над ним в предыдущей строке треугольника Паскаля. Например, (⁴₃) = (³₂) + (³₃). Поэтому строку треугольника Паскаля можно вычислить по значениям предыдущей строки. На рисунке 2 показано отношение между задачей (n-й строкой) и подзадачей ((n - 1)-й строкой).

Рис.2. Декомпозиция и восстановление строки треугольника Паскаля

Размер задачи - n. Таким образом, начальное условие соответствует n = 0, когда результат - это просто список, содержащий 1 ([1]). Для n = 1 нельзя применить рекурсивное правило (3.2). Поэтому поначалу кажется, что необходимо дополнительное начальное условие для n = 1 с результатом ([1,1]). Но поскольку все строки для n > 0 начинаются и заканчиваются с 1, эти элементы можно включить в рекурсивное условие по умолчанию. Таким образом, особое начальное условие для n = 1 становится излишним.

Пример 4.16. Функция, генерирующая n-ю строку треугольника Паскаля

1
2
3
4
5
6
7
8
9
10

def pascal(n):
    if n == 0:
        return [1]
    else:
        row = [1]
        previous_row = pascal(n - 1)
        for i in range(len(previous_row) - 1):
            row.append(previous_row[i] + previous_row[i + 1])    
        row.append(1)
        return row

Архив с файлом можно взять здесь.

В частности, предполагается, что в рекурсивном условии известно решение подзадачи, вычисляющей все элементы строки, кроме крайних (их можно просто добавлять, не вычисляя). В примере 4.16 приведено возможное решение задачи. Рекурсивное условие начинается с добавления 1 в итоговый список (строку). Строка 6 вычисляет результат подзадачи размера n - 1, а в строках 7 и 8 в цикле for пары целых чисел подзадачи складываются (как показано на рисунке 2) и их сумма добавляется к результату. В заключение в конец строки добавляется 1, на чём и заканчивается решение.

На следующем шаге мы рассмотрим резистивную цепь.

Предыдущий шаг Содержание Следующий шаг