На этом шаге мы обсудим реализацию такого алгоритма.

Первый шаг заключается в определении размера задачи, который, очевидно, равен количеству m цифр исходного числа n. Начальное условие выполняется, когда n состоит из одной цифры (то есть n < 10), а его результат - это результат сравнения (n = d). Допустим пока, что это - единственное начальное условие.

Рекурсивное условие будет довольно громоздким, если выражать значение каждой цифры через значение n. Поэтому можно применить иное обозначение, обсуждавшееся на 27 шаге. В частности, пусть d_m-1 ... d₁d₀ - последовательность из m цифр числа n по основанию 10. Тогда можно создать следующую схему с уменьшением размера задачи на 1 путём деления исходного числа n на 10 с отбрасыванием его наименьшей значащей цифры:

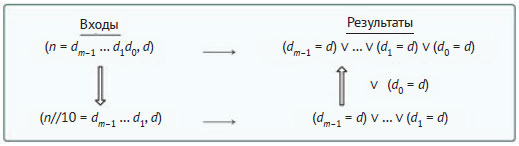
где ∨ обозначает логическую операцию ИЛИ (дизъюнкцию). Из схемы ясно видно, что если d - цифра n, то она либо входит в n//10 (то есть в результат рекурсивного вызова), либо равна d₀.

В схеме допускаются и другие обозначения с использованием слов или выражений, не вполне корректных с логической или математической точки зрения. Например, можно воспользоваться явно неподходящим здесь символом принадлежности ∈, который применяется только к множествам. Так, d ∈ n на самом деле будет означать принадлежность цифры d множеству цифр числа n. Несмотря на это, схема выполняет свое назначение - точно определить рекурсивное условие функции.

В примере 5.1 приведён код, реализующий искомую функцию, где n%10 - наименьшая значащая цифра n. Заметьте, что метод - линейно-рекурсивный, так как функция вызывает себя лишь раз и должна обработать результат подзадачи (то есть вычислить результат логического выражения с операцией or). Кроме того, если условие (n%10 == d) истинно, то компилятор или интерпретатор с "закорачиванием" (short-circuit) автоматически возвращал бы значение True, не вызывая contains_digit(n//10, d). В частности, использование "закорачивания" позволяет избегать ненужных вычислений согласно свойствам логических операций: True ∨ b = True и False ∧ b = False, где b - некоторое логическое выражение. Поскольку в этих случаях результат операции не зависит от значения b, то b можно не вычислять вообще.

Пример 5.1. Линейно-рекурсивная логическая функция, определяющая наличие в неотрицательном целом числе n заданной цифры d

1
2
3
4
5

def contains_digit(n, d):
    if n < 10:
        return n == d
    else:
        return (n % 10 == d) or contains_digit(n // 10, d)

Архив с файлом можно взять здесь.

На следующем шаге мы рассмотрим алгоритм хвостовой рекурсии.

Предыдущий шаг Содержание Следующий шаг