На этом шаге мы приведем реализацию такого алгоритма.

Большинство языков программирования поддерживает так называемое "закорачивание". Если его реализовать в дополнительном начальном условии, то это приведёт к хвостовому рекурсивному алгоритму. В частности, для этой задачи алгоритм может вернуть True, как только обнаружит цифру d в числе n. Поэтому можно вернуть True, если последняя цифра n равна d (то есть если n % 10 = d). Взглянув на это начальное условие, можно убедиться, что в рекурсивном условии n % 10 = d₀ ≠ d. Поэтому рекурсивная схема теперь будет такой:

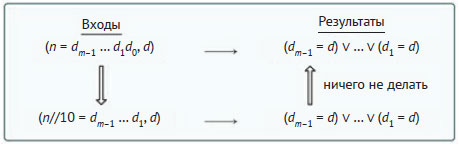
Она подразумевает, что результат подзадачи - это в точности результат исходной задачи и функция может вернуть результат рекурсивного вызова, не обрабатывая его. Вместе с начальными условиями она приводит к хвостовому рекурсивному алгоритму, который можно закодировать, как показано в примере 5.2.

Пример 5.2. Хвостовая рекурсивная логическая функция, определяющая, содержит ли неотрицательное целое число n цифру d

1
2
3
4
5
6
7

def contains_digit_tail(n, d):
    if n < 10:
        return n == d
    elif n % 10 == d:
        return True
    else:
        return contains_digit_tail(n // 10, d)

Архив с файлом можно взять здесь.

Важно понимать, что хотя выбранная декомпозиция делит входной параметр n на константу 10, размер задачи уменьшается всего на 1. Временная сложность алгоритма является логарифмом от числа n, но линейно зависит от количества его цифр m.

Наконец, эта задача имеет аналогии, опирающиеся на такие структуры данных, как списки, массивы и т. д., поскольку они тоже представляют собой последовательности элементов. Например, эта задача очень похожа на задачу о принадлежности некоторого символа строке или некоторого элемента списку. Хотя коды могут быть разными, но основное рассуждение, по сути, то же.

На следующем шаге мы рассмотрим рекурсивную реализацию алгоритма сравнения строк.

Предыдущий шаг Содержание Следующий шаг