На этом шаге мы рассмотрим особенности реализации такого поиска.

    Если исходный список a уже отсортирован, то найти в нём нужный элемент можно гораздо быстрее. Пусть список отсортирован в порядке возрастания, то есть a_i ≤ a_i+1 для i = 0, ..., n - 2. Задача может быть решена за время Ο(log n) алгоритмами "двоичного поиска". Основная идея таких методов (а они могут быть разными) заключается в последовательном делении размера задачи пополам. Рисунок 1 иллюстрирует декомпозицию задачи.

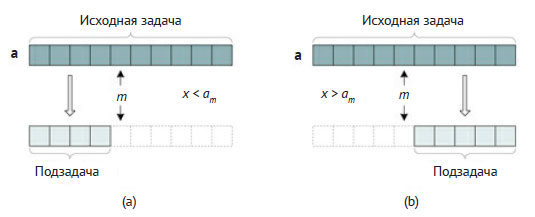
Рис.1. Декомпозиция для алгоритмов двоичного поиска

    Сначала алгоритмы вычисляют средний индекс m. Если x = a_m, они заканчивают работу в начальном условии, возвращая m. Иначе, поскольку список отсортирован, можно продолжить поиск x в одном из двух подсписков - справа или слева от m. В частности, если x < a_m, то x не может оказаться в правом подсписке [a_m, ..., a_n-1], и методы могут продолжить поиск x в левом подсписке [a₀, ..., a_m-1], как показано на рисунке 1(a). Аналогично, если x > a_m, то x может появиться только в [a_m+1, ..., a_n-1], как показано на рисунке 1(b). В сущности, этот подход делит размер задачи (n) пополам. Поэтому время выполнения будет определяться формулой (3.20), то есть в самом худшем случае методы будут выполняться за логарифмическое время от n. Наконец, функции возвращают -1 (в начальном условии), если список пуст.

    Подобно функциям линейного поиска в примерах 5.6 и 5.7, методы двоичного поиска должны включать дополнительные входные параметры для указания индексов исходного списка. Например, рассмотрим поиск 8 в списке [1, 3, 3, 5, 6, 8, 9]. Если в рекурсивном вызове функции мы передаём ей только подсписок [6, 8, 9], то в нём 8 теперь имеет индекс 1, тогда как в исходном списке значение 8 находится в позиции 5. Таким образом, нужно указать, что первый индекс подсписка должен быть именно 5. Другими словами, нужно определить дополнительный параметр - начальную позицию подсписка в исходном списке. В примере 5.8 приведена реализация метода, который включает не только этот параметр (lower), но и ещё один параметр (upper) - конечный индекс подсписка в исходном списке. Таким образом, lower и upper просто задают границы подсписка внутри а. Параметр upper в Python не обязателен, поскольку для определения верхнего индекса подсписка надо использовать длину списка. Однако код в примере 5.8 проще в том смысле, что требует меньше арифметических операций, не передаёт сам себе подсписок (рекурсивные вызовы используют весь список а) и показывает, как можно реализовать метод в других языках программирования, где длина списков не доступна напрямую. В частности, если lower больше upper, то список пуст, а метод возвращает -1. В противном случае функция проверяет начальное условие x = a_m. Если оно неверно, метод выполняет один из двух рекурсивных вызовов (с соответствующим подсписком) в зависимости от условия x < a_m. Наконец, метод-оболочка используется для инициализации индексов lower и upper значениями 0 и n - 1 соответственно.

def binary_search(a, x, lower, upper):
    if lower > upper:  # empty list
        return -1
    else:
        middle = (lower + upper) // 2

        if x == a[middle]:
            return middle
        elif x < a[middle]:
            return binary_search(a, x, lower, middle - 1)
        else :
            return binary_search(a, x, middle + 1, upper)    


def binary_search_wrap(a, x):
    return binary_search(a, x, 0, len(a) - 1)

    Со следующего шага мы начнем рассматривать двоичные деревья поиска.

Предыдущий шаг Содержание Следующий шаг