На этом шаге мы приведем общие сведения об этой структуре данных.
Двоичные (бинарные) деревья поиска - это структура данных, используемая для хранения элементов данных, каждому из которых назначен определенный ключ (будем считать ключи уникальными), подобно ключами в словаре языка Python. Это - важная структура данных, позволяющая эффективно выполнять такие операции, как поиск, вставка или удаление элементов. Данные в каждом узле двоичного дерева - это пара (ключ, элемент), а его узлы упорядочены по значению ключей, которые можно сравнивать операцией < или некоторой равнозначной ей функцией (то есть полное бинарное отношение предшествования). В частности, для любого узла дерева каждый ключ левого поддерева меньше ключа этого узла, тогда как все ключи правого поддерева больше ключа этого узла. Это основное "свойство двоичного дерева поиска", подразумевающее, что каждое поддерево двоичного дерева поиска - тоже двоичное дерево поиска.
Например, эта структура данных может использоваться для хранения информации о днях рождения. На рисунке 1 приведено двоичное дерево, позволяющее находить дни рождения семи человек по их именам-строкам, которые мы будем считать уникальными (для уникальной идентификации каждого человека можно, конечно, добавить ещё фамилии или прозвища).
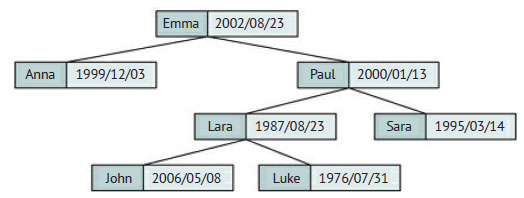
Рис.1. Двоичное дерево поиска с информацией о днях рождения
Ключи могут быть строками, поскольку их тоже можно сравнивать, например, в лексикографическом порядке (в Python можно просто воспользоваться операцией <). Поэтому имена в двоичном дереве поиска отсортированы так же, как в обычном словаре. Например, если взять корневой узел "Emma", то можно заметить, что все имена в его левом поддереве располагаются в словаре до него, а все имена в правом поддереве - после него. Более того, этим свойством обладают все узлы двоичного дерева поиска.
Прежде чем реализовать двоичное дерево поиска, нужно решить, как его представить. Существует несколько способов (один из наиболее общих подходов - воспользоваться объектно-ориентированными возможностями, определив, например, класс "узел дерева"), но здесь мы будем использовать обычные списки. В частности, каждый узел дерева будет списком из четырех элементов: ключа, элемента, левого и правого поддеревьев, где поддеревья - это тоже двоичные деревья. Таким образом, двоичное дерево на рисунке 1 представлялось бы следующим списком:
[Emma, 2002/08/23, [Anna, 1999/12/03, [], []], [Paul, 2000/01/13,
[Lara, 1987/08/23, [John, 2006/05/08, [], []],
[Luke, 1976/07/31, [], []]], [Sara, 1995/03/14, [], []]]], (5.1)
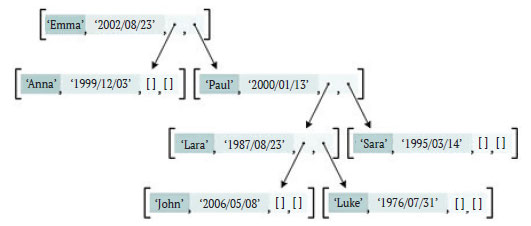
Рис.2. Двоичное дерево поиска (см. рис. 1), где каждый узел - список из четырёх элементов: имени (строка), дня рождения (строка), левого поддерева (список) и правого поддерева (список)
На следующем шаге мы рассмотрим организацию поиска элемента.
