На этом шаге мы рассмотрим особенности решения указанной задачи.

Цель следующей задачи - найти в двоичном дереве поиска элемент с заданным ключом k и получить его значение. Можно предположить, что размер задачи - высота дерева. Тривиальное начальное условие выполняется, когда список, представляющий двоичное дерево, пуст. В этом случае алгоритм может просто вернуть None. Есть другая ситуация, когда алгоритм может выдать результат, не выполняя рекурсивного вызова. Если ключ корневого узла равен k, то элемент сразу же найден и является результатом решения задачи. Таким образом, в рекурсивных условиях нужно убедиться, что корневой узел не содержит искомого элемента.

Цель следующего нашего шага - найти соответствующую декомпозицию задачи, уменьшающую ее размер. Нам уже известно, что деревья составляются рекурсивно из поддеревьев. Таким образом, нужно произвести поиск элемента в двух поддеревьях двоичного дерева. Это гарантирует уменьшение размера задачи на 1, так как корневой узел уже проверен. Однако легко видеть, что в этой задаче можно также избежать поиска во всем поддереве. Если ключ k меньше ключа корневого узла (k_root), то понятно, что согласно свойству двоичного дерева поиска искомого элемента не может быть в правом поддереве. Аналогично, если k > k_root, элемента не может быть в левом поддереве. Рисунок 1 иллюстрирует эту идею, где x_root - элемент, сохранённый в корневом узле.

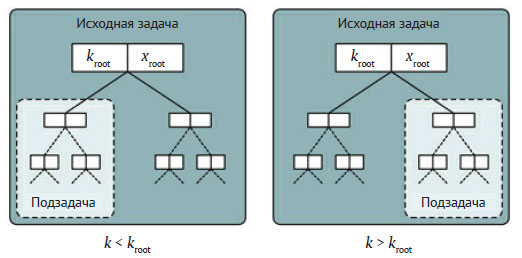
Рис.1. Декомпозиция для некоторых алгоритмов поиска в двоичном дереве

Понятно, что для этой частной задачи существует два рекурсивных условия. Если k < kroot, метод должен продолжить поиск в левом поддереве посредством рекурсивного вызова, тогда как если k > kroot, он должен искать элемент в правом поддереве. В примере 5.9 приведена реализация алгоритма поиска, где каждый узел двоичного дерева - это список из четырёх компонентов, как описано на предыдущем шаге.

Пример 5.9. Алгоритм поиска элемента с заданным ключом в двоичном дереве

1
2
3
4
5
6
7
8
9

def bst_search(T, key):
    if T == []:
        return None
    elif T[0] == key:
        return T[1]  # return the root item
    elif key < T[0]:
        return bst_search(T[2], key)  # search in left subtree
    else:
        return bst_search(T[3], key)  # search in right subtree

Архив с файлом можно взять здесь.

В итоге временная стоимость алгоритма определяется в самом худшем случае высотой двоичного дерева. Если дерево сбалансировано (то есть имеет примерно равное количество узлов на одном и том же уровне в левых и правых поддеревьях), то время его работы - (log n), где n - число узлов в дереве, поскольку при каждом рекурсивном вызове он пропускает примерно половину узлов. Но если дерево имеет линейную структуру, то оценка времени работы алгоритма - Ο(n).

На следующем шаге мы рассмотрим вставку элемента.

Предыдущий шаг Содержание Следующий шаг