На этом шаге мы рассмотрим эту схему.

Простая идея заключается в просмотре всего входного списка с целью построить:

(1) новый список из элементов, не бОльших опорного, и
(2) другой список из элементов, бОльших опорного.

После чего их можно объединить, вставив между ними опорный элемент.

Так как обе задачи очень похожи, мы разберём только первую. В частности, вход задачи - список длины n и некоторое значение х, исполняющее роль опорного элемента. Её размер - очевидно, длина списка. Начальное условие возникает при пустом входном списке, когда алгоритм просто возвращает пустой список. Для вывода рекурсивного условия применим декомпозицию с уменьшением размера задачи на 1 путём отбрасывания первого элемента списка. В этом случае можно сформировать следующие рекурсивные схемы в зависимости от соотношения между 1-м и опорным элементами списка. Если 1-й элемент не больше опорного, то схема для конкретного списка может быть такой:

Ясно, что алгоритм должен объединить 1-й элемент списка с результатом подзадачи. Напротив, если 1-й элемент больше опорного, то схема будет такой:

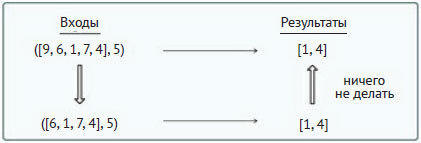
В этом случае алгоритм просто должен вернуть решение (список) подзадачи. В примере 5.11 приведён линейно-рекурсивный код, решающий обе задачи (обратите внимание, что в рекурсивных условиях, выполняющих объединение списков, вызов функции не является последним действием метода).

Пример 5.11. Вспомогательные методы для разбиения списка

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def get_smaller_than_or_equal_to(a, x):
    if a == []:
        return []
    elif a[0] <= x:
        return [a[0]] + get_smaller_than_or_equal_to(a[1:], x)    
    else:
        return get_smaller_than_or_equal_to(a[1:], x)


def get_greater_than(a, x):
    if a == []:
        return []
    elif a[0] > x:
        return [a[0]] + get_greater_than(a[1:], x)    
    else:
        return get_greater_than(a[1:], x)

Архив с файлом можно взять здесь.

Время выполнения методов можно оценить как:

            1,            если n = 0,
    T(n) = 
            T(n - 1) + 1, если n > 0.

Это значит, что время выполнения методов линейно относительно n. Наконец, функции можно заменить выражениями языка Python, реализующими "фильтры". В частности, функции get_smaller_than_or_ equal_to(a, x) и get_greater_than(a, x) возвращают те же списки, что и выражения [y for y in a if y <= x] и [y for y in a if y > x] соответственно.

На следующем шаге мы рассмотрим метод разбиения Хоара.

Предыдущий шаг Содержание Следующий шаг