На этом шаге мы рассмотрим этот метод и приведем приложения, иллюстрирующие его реализацию.

    В примере 5.12 приведена итерационная версия алгоритма разбиения Хоара. В частности, он выполняет внутреннее разбиение списка a на подсписки, которые определяются своими нижним и верхним индексами.

def partition_Hoare(a, lower, upper):
    if upper >= 0:
        middle = (lower + upper) // 2
        pivot = a[middle]
        a[middle] = a[lower]
        a[lower] = pivot

        left = lower + 1
        right = upper

        finished = False
        while not finished:
            while left <= right and a[left] <= pivot:    
                left = left + 1

            while a[right] > pivot:
                right = right - 1

            if left < right:
                aux = a[left]
                a[left] = a[right]
                a[right] = aux

            finished = left > right

        a[lower] = a[right]
        a[right] = pivot

        return right

    Сначала метод выбирает опорный элемент (в данном случае - в середине подсписка) и меняет его с первым элементом подсписка (строки 3-6). Затем он устанавливает левый индекс на второй позиции подсписка, а правый - на последней (строки 8 и 9). После чего метод запускает основной цикл алгоритма. В нём он последовательно увеличивает левый индекс, пока тот не укажет на элемент, больший, чем опорный (строки 13 и 14). Таким же образом он уменьшает правый индекс, пока тот не укажет на элемент, не больший опорного (строки 16 и 17). После этого (строки 19-22) алгоритм меняет элементы, на которые ссылаются левый и правый индексы (если левый индекс меньше правого). Этот процесс повторяется до тех пор, пока индексы не пересекутся (то есть пока левый индекс не станет больше правого, что проверяется в строке 24). В конце цикла элементы до правого индекса будут не больше опорного, а элементы после левого индекса (и до конца подсписка) будут больше опорного. В заключение процедура разбиения меняет местами элемент с правым индексом и опорный (строки 26 и 27) и возвращает его окончательную позицию. На рисунке 1 приведён конкретный пример метода разбиения.

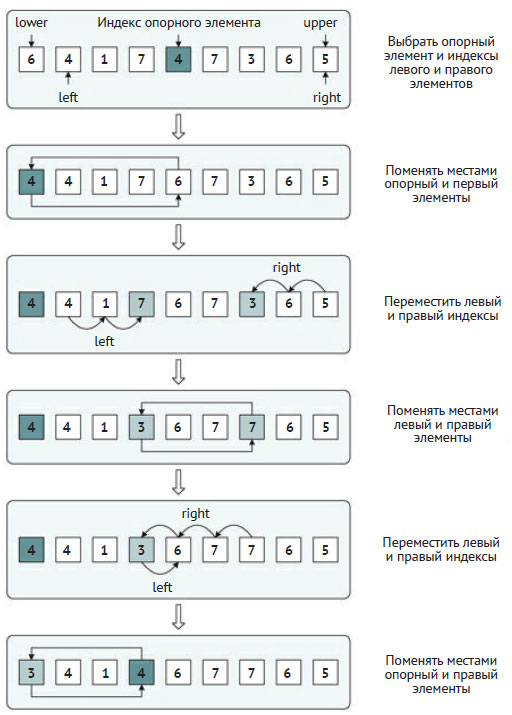
Рис.1. Пример метода разбиения Хоара

    Рассмотрим теперь алгоритм хвостовой рекурсии, который должен заменить основной цикл в схеме разбиения Хоара. Для заданных входного списка а, начальных значений левого и правого индексов, а так же опорного элемента метод должен, подобно циклу в методе Хоара, разбить список и вернуть заключительную позицию правого индекса. Размер задачи - это разность между левым и правым индексами, поскольку именно она определяет количество операций увеличения и уменьшения индексов до их пересечения. Именно в тот момент, когда левый индекс становится больше правого, выполняется начальное условие, а метод просто возвращает правый индекс.

    В рекурсивном условии мы будем сокращать размер задачи путём увеличения левого индекса и/или уменьшения правого. Возможны два разных сценария, приведённых на рисунке 2, где p - опорный элемент, left и right - соответственно левый и правый индексы.

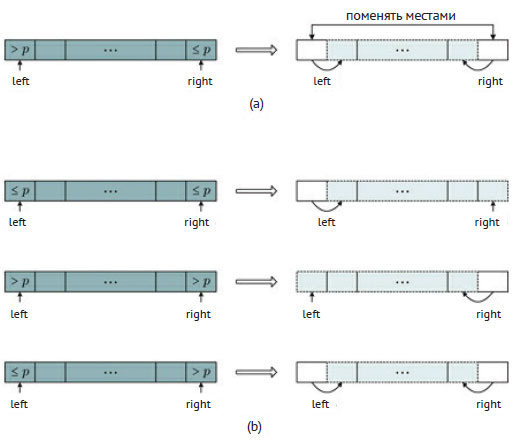
Рис.2. Декомпозиция задачи о разбиении Хоара

    Если a[left] > p и a[right] ≤ p, то сначала метод должен поменять местами элементы с этими индексами и только после этого выполнить вызов функции с продвижением обоих индексов, как показано на рисунке 2(a). Это приводит к первому рекурсивному условию, уменьшающему размер задачи на две единицы. Если предыдущее условие не выполняется, метод не поменяет местами элементы, а изменит, по крайней мере, один из индексов (уменьшив тем самым размер задачи), как показано на рисунке 2(b). Если a[left] ≤ p, он увеличит левый индекс, а если a[right] > p - уменьшит правый. После этого метод вызывает сам себя с новыми значениями индексов. В примере 5.13 приводится соответствующий код вместе с методом-оболочкой, завершающим алгоритм разбиения. Отметим, что он идентичен примеру 5.12, цикл которого заменён вызовом рекурсивной функции. Наконец, метод работает за время Ο(n), так как время выполнения рекурсивного метода может быть в самом худшем случае оценено рекуррентным соотношением T(n) = T(n - 1) + 1.

def partition_Hoare_rec(a, left, right, pivot):
    if left > right:
        return right
    else:
        if a[left] > pivot and a[right] <= pivot:    
            aux = a[left]
            a[left] = a[right]
            a[right] = aux
            return partition_Hoare_rec(a, left + 1,
                                       right - 1, pivot)
        else:
            if a[left] <= pivot:
                left = left + 1
            if a[right] > pivot:
                right = right - 1
            return partition_Hoare_rec(a, left, right, pivot)    


def partition_Hoare_wrapper(a, lower, upper):
    if upper >= 0:
        middle = (lower + upper) // 2
        pivot = a[middle]
        a[middle] = a[lower]
        a[lower] = pivot

        right = partition_Hoare_rec(a, lower + 1, upper, pivot)

        a[lower] = a[right]
        a[right] = pivot

        return right

    На следующем шаге мы рассмотрим алгоритм quickselect.

Предыдущий шаг Содержание Следующий шаг