На этом шаге мы рассмотрим решение этой задачи.

    В этой задаче лесорубу нужно заготовить w погонных метров древесины на лесном участке из n деревьев. У него есть специальная машина, пилу которой можно установить на любую высоту h так, чтобы срезать деревья выше этой высоты. Пусть w - целое число (не превосходящее суммарной высоты всех деревьев на участке), а высоты n деревьев (тоже целочисленные) заданы в списке t. Цель задачи - найти наибольшее значение h, которое позволит лесорубу заготовить по крайней мере (то есть с минимальным излишком) w погонных метров древесины. На рисунке 1 приведён пример задачи для n = 20 деревьев, где высота самого высокого дерева H = 12.

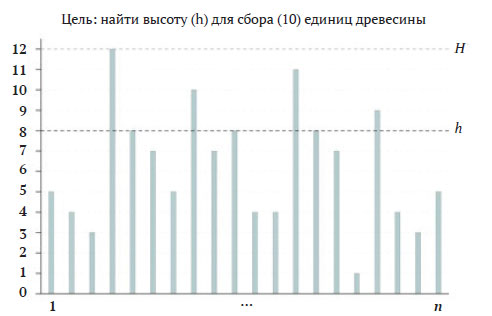
Рис.1. Пример задачи лесоруба

    Если нужно заготовить 10 погонных метров леса, то лесоруб должен установить высоту пилы h = 8, чтобы спилить в точности 10 погонных метров. И даже если нужно заготовить 7, 8 или 9 погонных метров леса, то оптимальная высота h всё равно была бы равна 8. Несмотря на то что лесоруб заготовил бы несколько больше погонных метров древесины, h не должна быть больше, поскольку срез на высоте 9 дал бы только 6 погонных метров древесины.

    Задача представляет интерес с алгоритмической точки зрения, поскольку может быть решена несколькими способами. Например, деревья можно сначала отсортировать в порядке убывания их высот, а затем спиливать от самого высокого до самого низкого до получения оптимального результата. Этот подход работал бы за время Ο(n log n), если бы мы применяли такие общие алгоритмы сортировки, как сортировка слиянием или quicksort. Так как высоты - это целые числа, можно применить линейные алгоритмы сортировки за линейное время, как в методе сортировки подсчётом, который привел бы к решению, работающему за время Ο(n + H). Таким образом, при малых значениях H этот подход мог бы быть наиболее эффективным.

    Теперь рассмотрим алгоритм решения задачи методом "двоичного поиска", который работает за время Ο(n log H) и не требует сортировки деревьев по высоте. Сразу отметим, что алгоритм начинает работу с h = H - 1, постепенно уменьшая её на 1 до получения нужного количества леса.

    Для простоты предположим, что метод вычисляет количество леса, полученное для каждой новой высоты h независимо от количества, полученного для других высот. Это значит, что вычисление количества леса, собранного с n деревьев, требует порядка n операций. Поэтому для решения всей задачи алгоритм потребовал бы Ο(nH) операций в самом худшем случае (для каждой из возможных высот H алгоритм должен будет выполнить n вычислений). В частности, количество леса, собранного для некоторой высоты h, может быть получено линейно-рекурсивной функцией из примера 5.16. В начальном условии, когда список высот деревьев пуст, метод возвращает ноль. Рекурсивное условие обрабатывает высоту первого дерева из списка. Если она больше h, то дерево будет спилено, а функция должна вернуть (за счёт рекурсивного вызова) разницу между высотой дерева t₀ и h плюс длина уже заготовленной с остальной части деревьев древесины. Если высота дерева не больше h, то дерево не спиливается, и метод может просто вернуть величину уже заготовленного леса.

def compute_wood(t, h):
    if t == []:
        return 0
    else:
        if t[0] > h:
            return t[0] - h + compute_wood(t[1:], h)    
        else:
            return compute_wood(t[1:], h)

    Вместо постепенного уменьшения h на 1 следующий алгоритм использует стратегию, подобную двоичному поиску элемента в списке или методу деления пополам. Идея состоит в том, чтобы начать поиск высоты h с середины интервала [0, H] и постепенно делить его пополам, пока не будет получено решение. Таким образом, метод получает в качестве параметров высОты деревьев, погонный метраж заготовляемой древесины, а также нижний и верхний пределы интервала поиска h.

    Размер задачи - это разность между верхним и нижним пределами (сначала равна H). Первое начальное условие выполняется, если их значения равны. В этом случае высота h будет именно этим значением. В противном случае алгоритм вычислит "среднюю" высоту как (целочисленное) среднее от нижнего и верхнего пределов. Если суммарная длина спиленной на этой средней высоте древесины равна w, то метод возвращает эту среднюю высоту во втором начальном условии.

    На рисунке 2 показана используемая в алгоритме декомпозиция задачи.

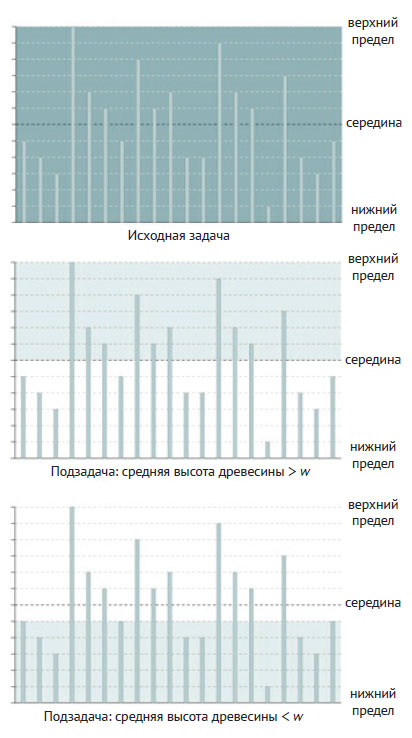
Рис.2. Декомпозиция задачи лесоруба

    Исходная задача показана вверху с учётом нижнего и верхнего пределов. После вычисления общей длины древесины, которая могла быть собрана при средней высоте (h_m), возможны два сценария. Первый сценарий имеет место, когда h_m превышает w. В этом случае можно, очевидно, исключить все высоты ниже h_m и продолжить поиск оптимальной высоты (рекурсивным вызовом), изменив нижний предел на h_m. Важно отметить, что h_m все еще может быть решением, так как собранный для h_m+1 лес может быть меньше необходимого количества w. Второй сценарий имеет место, когда собранный при h_m лес меньше w. В этом случае можно отказаться от всех высот выше средней, так как они не позволят лесорубу получить достаточного количества древесины. Поэтому соответствующее рекурсивное условие должно вызвать метод, заменив верхний предел h_m-1.

    Наконец, в предыдущей декомпозиции, когда верхний предел всего на единицу больше нижнего, средняя высота равна нижнему пределу. В этом случае первое рекурсивное условие не должно уменьшать размер задачи (пределы не должны меняться). Таким образом, чтобы работать должным образом, алгоритм нуждается в дополнительном начальном условии. Когда возникает такая ситуация, метод должен вернуть либо нижний, либо верхний предел. В частности, если количество леса, соответствующего верхнему пределу, не меньше w, то верхний предел - правильный результат. Иначе им будет нижний предел.

    В примере 5.17 приведён код, соответствующий упомянутым начальным и рекурсивным условиям.

def collect_wood(t, wood, lower, upper):
    middle_h = (lower + upper) // 2
    wood_at_middle = compute_wood(t, middle_h)

    if wood_at_middle == wood or lower == upper:    
        return middle_h
    elif lower == upper - 1:
        if compute_wood(t, upper) >= wood:
            return upper
        else:
            return lower
    elif wood_at_middle > wood:
        return collect_wood(t, wood, middle_h, upper)
    else:
        return collect_wood(t, wood, lower, middle_h - 1)     

    Наконец, на рисунке 3 приведена последовательность шагов алгоритма по решению задачи для конкретного примера на рисунке 1.

Рис.3. Шаги алгоритма двоичного поиска на примере задачи лесоруба для w = 10

    Шаг 1 соответствует начальному условию, когда нижний предел равен нулю, а верхний - H = max{t_i} для i = 1, ..., n. Шаги 2 и 3 соответствуют применению первого и второго рекурсивных условий соответственно. Наконец, шаг 4 соответствует дополнительному начальному условию, когда верхний предел (8) на 1 больше нижнего (7). Решение - h = 8, поскольку при такой высоте лесоруб получает требуемое количество леса (10 единиц).

    На следующем шаге мы рассмотрим алгоритм Евклида.

Предыдущий шаг Содержание Следующий шаг