На этом шаге мы рассмотрим рекурсивную реализацию этого алгоритма.

    Рассмотрим непрерывную действительную функцию f(x), определенную на интервале [a, b]. Алгоритм двоичного поиска (также известный как метод деления интервала пополам, половинного деления, бисекции или дихотомии) - это способ поиска приближения z корня f(x) на интервале (a, b). Напомним, что корень, или ноль f(x), - это значение r, для которого f(r) = 0.

    Входные параметры задачи - границы интервала a и b, где a ≤ b, функция f() и малое значение е > 0, задающее точность приближения, то есть выходной параметр функции z должен удовлетворять условию | z - r | ≤ е. Таким образом, чем меньше е, тем точнее приближение. Ещё одно обязательное условие - то, что f(a) * f(b) < 0. Это гарантия того, что корень находится внутри интервала (a, b). Наконец, приближение z определяется серединой интервала (a, b), то есть z = (a + b)/2.

    Метод последовательно делит пополам тот интервал, где должен быть корень. На рисунке 1 приведено несколько шагов этого процесса.

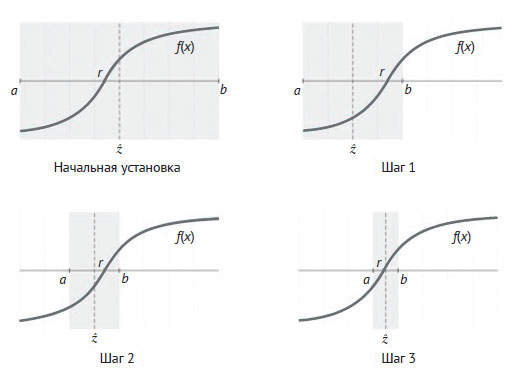
Рис.1. Несколько шагов алгоритма двоичного поиска корня

    В исходном положении корень расположен слева от первого приближения z или середины интервала (r < z), поэтому на следующем шаге граница b смещается ближе к этой середине. Точно так же на шаге 1 z < r, поэтому на следующем шаге a получит значение z. Эта процедура применяется многократно до тех пор, пока интервал не станет достаточно маленьким, чтобы обеспечить для z необходимую точность.

    Размер задачи зависит от длины отрезка [a, b], а начальное условие выполняется при b - a ≤ 2е, когда метод возвращает z = (a + b)/2. Заметим, что это условие обеспечивает выполнение условия | z - r | ≤ е, как видно по рисунку 2.

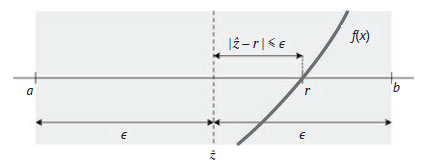
Рис.2. Начальное условие алгоритма двоичного поиска b - a ≤ 2е

    В частности, если z - середина отрезка [a, b], то расстояние между z и r не может быть больше е. Кроме того, метод может просто вернуть z, если f(z) = 0 (или f(z) достаточно мала).

    Декомпозиция задачи заключается в делении её размера пополам. Это достигается заменой одного из граничных значений отрезка [a, b] его серединой z. Поскольку знаки значений функции на концах отрезка должны быть противоположными, z должен заменить b, когда f(a) и f(z) имеют противоположные знаки. Иначе z заменяет a. Это приводит к хвостовому рекурсивному методу в примере 5.15, содержащему два рекурсивных условия. В коде используется функция f(x) = x² - 2, которая позволяет найти приближение √2, поскольку это корень f(x). Отметим, что начальный интервал [0, 4] содержит √2. Наконец, погрешность приближения будет не более 10^-10 (результат получится с точностью до девяти десятичных цифр после десятичной запятой).

def f(x):
    return x * x - 2


def bisection(a, b, f, epsilon):
    z = (a + b) / 2

    if f(z) == 0 or b - a <= 2 * epsilon:
        return z
    elif (f(a) > 0 and f(z) < 0) or (f(a) < 0 and f(z) > 0):    
        return bisection(a, z, f, epsilon)
    else:
        return bisection(z, b, f, epsilon)


# Print an approximation of the square root of 2
print(bisection(0, 4, f, 10 ** (-10)))

    На следующем шаге мы рассмотрим задачу лесоруба.

Предыдущий шаг Содержание Следующий шаг