На этом шаге мы разберем особенности решения этой задачи.

    В этой задаче (также известной как "проход по трясине") прямоугольное болото из квадратных участков задаётся матрицей A размерности n*m и начальной строкой r. Элементы матрицы (a_i,j) могут иметь только два значения - "суша" ("кочка") или "топь". Цель задачи - найти путь через болото (от левого его края до правого), начав с заданного на его левом краю участка суши a_r,0, согласно следующим правилам (см. рисунок 1(a)):

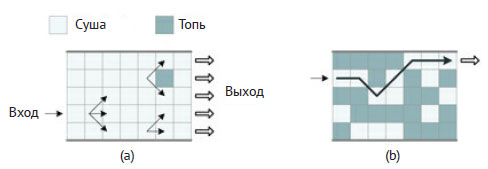
Рис.1. Задача о пути по болоту

• путь через болото может проходить только по суше;
• продвигаться можно только вправо и только по смежным участкам суши. Например, с участка a_i,j можно шагнуть только на участки a_i-1,j+1, a_i,j+1 или a_i+1,j+1. Отметим, что движение по вертикали запрещено. Путь не может пересекать нижнего и верхнего краёв болота;
• путь должен заканчиваться на любом участке суши на правом краю болота.

    Рисунок 1(b) показывает путь через болото, где участки суши и топи изображаются светлыми и темными квадратами соответственно.

    Можно предположить, что размер задачи - это ширина болота (m). В первом начальном условии метод может просто вернуть False, если r выходит за пределы болота (r < 0 или r > n) или если начальный участок a_r,0 - топь (отметим, что это последнее условие было бы ненужным, если бы мы сразу условились, что первый участок - это суша). Иначе функция должна будет вернуть True, если ширина болота равна 1 (это обеспечивается предыдущим начальным условием, проверяющим, что участок является сушей).

    В примере 7.1 приведена одна из многих возможных реализаций функции. Матрица (из пакета NumPy) содержит символы, где символ 'W' обозначает топь. Строки 2-5 определяют начальные условия. В строках 7, 8 и 9 метод определяет, можно ли перейти к a_r-1,1 (по диагонали вверх), a_r,1 (по горизонтали вправо) или a_r+1,1 (по диагонали вниз) соответственно.

def exists_path_swamp(A, r):
    if r < 0 or r >= A.shape[0] or A[r, 0] == 'W':
        return False
    elif A.shape[1] == 1:
        return True
    else:
        return (exists_path_swamp(A[:, 1:], r - 1) or    
                exists_path_swamp(A[:, 1:], r) or
                exists_path_swamp(A[:, 1:], r + 1))

    В рекурсивном условии задача разбивается на три подзадачи размера m - 1 (см. рисунок 2).

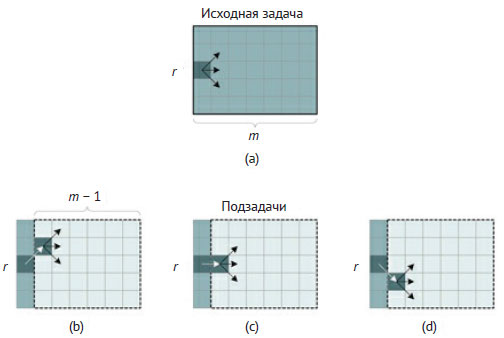
Рис.2. Декомпозиция задачи о пути через болото

    В частности, можно предположить, что нам известен правильный путь через болото, начинающийся с участков a_r-1,1, a_r,1 или a_r+1,1. Иными словами, можно считать, что нам известны решения трех меньших подзадач, возникающих после отбрасывания первого столбца болота и начинающихся с участков в строках r - 1, r и r + 1. Таким образом, рекурсивное условие будет состоять из трёх соответствующих подзадачам рекурсивных вызовов.

    Интересно выяснить, как влияют на алгоритм предварительные условия. В примере 7.2 есть предварительное условие для входа a_r,0 ≠ 'W'. Поэтому ему не нужна проверка a_r,0 = 'W' (см. строку 2 в примере 7.1). Кроме того, любой вызов метода, которому предшествует условный оператор, должен убедиться, что a_r,0 ≠ 'W'. В итоге эффективность кода возросла за счёт включения условных операторов в строках 10 и 17, которые устраняют лишние рекурсивные вызовы, если путь через болото уже найден. Например, если уже существует путь вверх по диагонали, то не нужно проверять другие направления - по горизонтали или вниз по диагонали.

def exists_path_swamp_alt(A, r):
    if A.shape[1] == 1:
        return A[r, 0] != 'W'
    else:
        if r == 0 or A[r - 1, 1] == 'W':
            diag_up = False
        else:
            diag_up = exists_path_swamp_alt(A[:, 1:], r - 1)    

        if not diag_up:
            if r == A.shape[0] - 1 or A[r + 1, 1] == 'W':
                diag_down = False
            else:
                diag_down = exists_path_swamp_alt(
                    A[:, 1:], r + 1)

            if not diag_down:
                if A[r, 1] == 'W':
                    horizontal = False
                else:
                    horizontal = exists_path_swamp_alt(
                        A[:, 1:], r)

    return diag_up or diag_down or horizontal    

    Наконец, в примерах 7.1 и 7.2 размер матрицы уменьшается явно - вызовом метода с параметром A[:, 1:]. Другая возможность состоит в том, чтобы всегда передавать матрицу n*m целиком и управлять размером задачи с помощью входного параметра, задающего столбец с, с которого метод должен начать поиск пути. При таком сценарии отправной точкой пути была бы a_r,c. В результате код оказался бы более общим, позволяя найти правильный путь через болото не только из его левого края, но и из любого участка суши a_r,c.

    На следующем шаге мы рассмотрим ханойскую башню.

Предыдущий шаг Содержание Следующий шаг