На этом шаге мы приведем рекурсивное решение этой задачи.

Игра "Ханойская башня" - одна из самых популярных задач для иллюстрации рекурсии. Несмотря на то что её можно решить с помощью относительно простых итерационных алгоритмов, она также допускает короткое и изящное рекурсивное решение, которое не только подчеркивает роль декомпозиции и индукции в рекурсии, но и демонстрирует их возможности при решении задач.

Игра состоит из трёх вертикальных стержней и n дисков, которые можно насадить на любой стержень, как показано на рисунке 1 для n = 7 дисков. Диски имеют разные радиусы, и можно считать, что радиус диска i равен i.

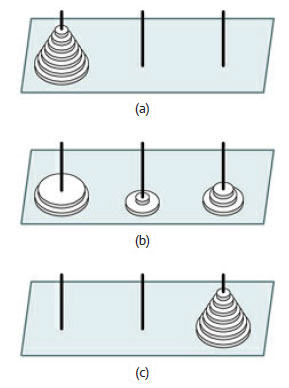
Рис.1. Головоломка "Ханойская башня"

В исходном положении все n дисков насажены на один из стержней в порядке убывания (индекса или радиуса), как показано на рисунке 1(a). Цель игры состоит в том, чтобы, используя третий (вспомогательный) стержень, переместить всю башню лежащих друг на друге дисков с сохранением их порядка следования с первого (начального) стержня на другой (конечный) стержень, руководствуясь следующими правилами:

только один диск может быть перемещён за один раз;
при каждом перемещении с одного из стержней снимается верхний диск и насаживается на другой стержень;
на любом стержне больший диск не может лежать на меньшем.

На рисунке 1(b) приведено положение дисков на некотором промежуточном шаге после выполнения нескольких перемещений, а на рисунке 1(c) - заключительное состояние дисков, когда задача решена и все диски находятся на нужном стержне.

Размер задачи определяется количеством дисков. Начальное условие возникает при n = 1, когда решение тривиально и заключается в перемещении диска с исходного стержня на заключительный (см. рисунок 2).

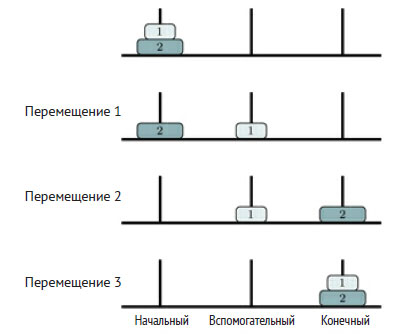
Рис.2. Решение головоломки "Ханойская башня" с количеством дисков n = 2

На первом шаге меньший диск переносится на вспомогательный стержень, что позволяет переместить больший диск на конечный стержень. На последнем шаге меньший диск просто перемещается на конечный стержень.

Можно доказать, что минимальное число перемещений, необходимое для решения задачи с n дисками, равно 2ⁿ - 1. Для n = 4 задача может быть решена за 15 перемещений (см. рисунок 3).

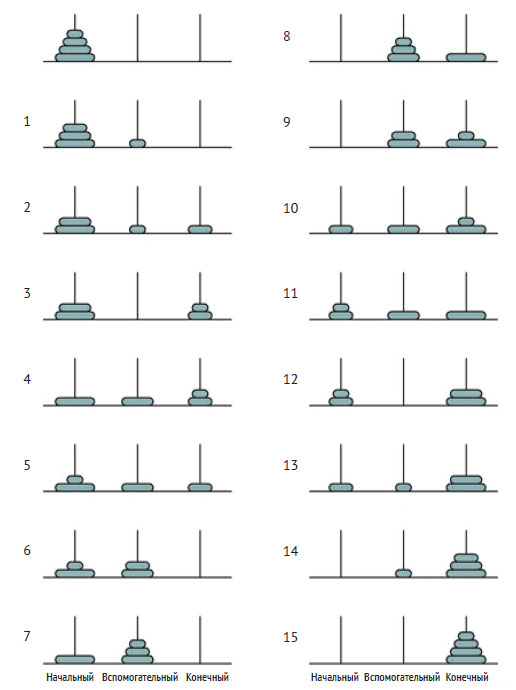
Рис.3. Решение головоломки "Ханойская башня" с количеством дисков n = 4

Несмотря на то что число перемещений растёт экспоненциально относительно n, при использовании рекурсии сложность задачи, в сущности, та же, что для случая n = 2. Самые интересные конфигурации дисков при n = 4 - после перемещений 7 и 8. Заметим, что после 7-го перемещения на вспомогательном стержне находится (n - 1)-й диск. Эта комбинация нужна для перемещения наибольшего диска на конечный стержень. Таким образом, первые семь шагов состоят из решения задачи для n - 1 = 3 дисков, когда цель заключается в перемещении этих трёх дисков с начального стержня на вспомогательный при посредстве конечного стержня. Другими словами, конечный и вспомогательный стержни меняются ролями. Восьмое перемещение - главная операция по перемещению наибольшего диска. После того как он помещён на конечный стержень, на вспомогательном стержне находится стопка из n - 1 дисков, которую нужно переместить на конечный стержень. Таким образом, семь оставшихся шагов - это решение другой задачи из n - 1 дисков, когда роли вспомогательного и конечного стержней меняются местами. Этот вывод, опирающийся на декомпозицию задачи и индукцию, показан на рисунке 4.

Рис.4. Декомпозиция задачи "Ханойская башня"

В частности, декомпозиция рассматривает две задачи размером n - 1, решение которых состоит из трёх шагов. Если на первом и третьем шагах решается одна из подзадач, то на втором шаге наибольший диск перемещается на конечный стержень. Следовательно, рекурсивное решение может опираться на индукцию, чтобы предположить, что мы можем переместить всю стопку из n - 1 дисков за один шаг (соответствующий рекурсивному вызову). Отметим, что в этом случае решение концептуально подобно случаю n = 2. В частности, отметим подобие рисунков 2 и 4. Оба решения состоят из трёх шагов, когда диск 1 заменяется стопкой из n - 1 дисков на рисунке 4 (а диск 2 играет ту же роль, что диск n).

В примере 7.3 приведена реализация процедуры, которая выводит на экран протокол перемещений дисков.

Пример 7.3. Процедура решения задачи "Ханойская башня"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def towers_of_Hanoi(n, o, d, a):
    if n == 1:
        print('Переместить диск', n, 'со стержня', o, 'на стержень', d)    
    else:
        towers_of_Hanoi(n - 1, o, a, d)
        print('Переместить диск', n, 'со стержня', o, 'на стержень', d)
        towers_of_Hanoi(n - 1, a, d, o)


def towers_of_Hanoi_alt(n, o, d, a):
    if n > 0:
        towers_of_Hanoi_alt(n - 1, o, a, d)
        print('Переместить диск', n, 'со стержня', o, 'на стержень', d)
        towers_of_Hanoi_alt(n - 1, a, d, o)


towers_of_Hanoi(4, 'O', 'D', 'A')

Архив с файлом можно взять здесь.

Последняя строка кода просто вызывает метод, который выводит протокол перемещений (см. рисунок 5) для n = 4.

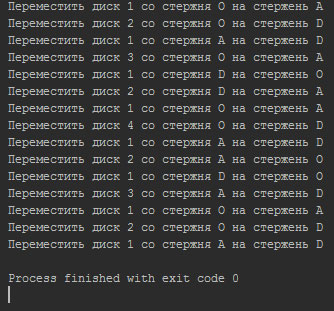
Рис.5. Результат процедуры из примера 7.3 при решении задачи "Ханойская башня" с количеством дисков n = 4

Параметры, относящиеся к стержням, нужны для правильного задания отдельных подзадач (включая исходную). В коде также приведена альтернативная процедура, рассматривающая начальное условие для n = 0, когда ничего делать не нужно.

Со следующего шага мы начнем рассмотривать обходы дерева.

Предыдущий шаг Содержание Следующий шаг