На этом шаге мы рассмотрим рекурсивное решение этой задачи.

В этой задаче в заданной исходной строке s = s₀s₁... s_n-2s_n-1 длины n, где s_i - её символы, нужно найти самую длинную подстроку-палиндром. Если таких палиндромов несколько, алгоритм возвращает любой из них. Важно понимать, что подстрока - это непрерывная последовательность элементов s, дабы не путать её с понятием подпоследовательности, элементы которой не обязательно идут подряд. Кроме того, это задача оптимизации, цель которой - в достижении максимального значения некоторой функции от исходной строки. Такие задачи обычно решаются методами "динамического программирования", которые применяются к определенному классу задач оптимизации.

Размер задачи - это длина исходной строки n. Наименьшие её экземпляры - это строки длины 0 (пустая строка) и 1 (строка из одного символа), когда алгоритм в начальном условии просто возвращает входную строку. Задачу можно упростить, отказавшись от крайних символов строки. Таким образом, декомпозиция исходной задачи на рисунке 1(a) предполагает решение двух подзадач на рисунках 1(b) и 1(c).

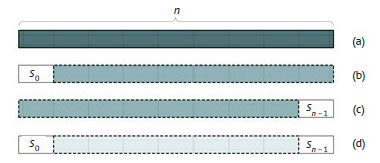
Рис.1. Декомпозиция задачи поиска в строке самого длинного палиндрома

Понятно, что если самая длинная подстрока-палиндром не содержит самый левый символ (s₀) исходной строки, то результатом будет выход метода, применённого к оставшейся подстроке (s_1...n-1), независимо от того, принадлежит ли s_n-1 решению. Точно так же, если самая длинная подстрока-палиндром не содержит s_n-1, алгоритм должен вернуть самую длинную подстроку-палиндром строки s_0...n-2. Наконец, вся входная строка может оказаться палиндромом.

В примере 7.6 приведена реализация рекурсивного метода.

Пример 7.6. Поиск самого длинного палиндрома в строке

1
2
3
4
5
6
7
8
9
10
11

def longest_palindrome_substring(s):
    n = len(s)
    if is_palindrome(s):
        return s
    else:
        s_aux_1 = longest_palindrome_substring(s[1:n])
        s_aux_2 = longest_palindrome_substring(s[0:n - 1])    
        if len(s_aux_1) > len(s_aux_2):
            return s_aux_1
        else :
            return s_aux_2

Архив с файлом можно взять здесь.

Так как эта задача подобна задаче поиска самого длинного палиндрома-подсписка, код работает так же, как если бы вход был списком. Если вход s - палиндром (см. 70 шаг), то результатом будет просто s, который, естественно, включает и пустую строку, и строку из одного элемента. В противном случае алгоритм ищет самый длинный палиндром в двух подстроках длины n - 1 и возвращает самое длинное решение. Оценку времени его выполнения можно определить как

            1,                   если 0 ≤ n ≤ 1,
    T(n) =                                            
            2T(n - 1) + n/2 + 1, если n > 1,

где n/2 - слагаемое, связанное с вызовом is_palindrome(). Нерекурсивное выражение T(n) = (7/4)2ⁿ - n/2 - 2. Таким образом, T(n) ∈ Θ(2ⁿ) имеет экспоненциальный рост.

Понятно, что рекурсивный алгоритм неэффективен, так как задача может быть решена "в лоб" за время Ο(n³). Отметим, что существует порядка n² подстрок (их можно задать двумя граничными индексами, управляемыми двумя циклами), требующих порядка n операций для определения, является ли строка палиндромом. Неэффективность примера 7.6 происходит из-за наличия многочисленных идентичных перекрывающихся подзадач. Например, оба рекурсивных вызова на рисунке 1(d) решают подзадачу длины n - 2, что влечёт за собой повторение идентичных и потому избыточных действий. Более того, меньшие идентичные подзадачи решаются за показательное время. Тем не менее такие рекурсивные решения полезны на практике, так как их разработка может быть первым шагом к проектированию более эффективных алгоритмов. Позже мы обсудим, как избежать перекрытия подзадач в рекурсивных решениях с помощью подхода, известного как мемоизация, или применения динамического программирования, которое является выдающимся методом проектирования алгоритмов. Основанные на динамическом программировании решения этой задачи могут работать за время Ο(n²). Наконец, было разработано несколько алгоритмов, способных решить эту задачу за линейное время.

Итак, в примере 7.6 используется функция is_palindrome() для определения, является ли строка палиндромом. Следующий пример заменяет эту функцию другим рекурсивным вызовом. Очевидно, строка s длины n является палиндромом, если самая длинная её подстрока-палиндром имеет длину n. Таким образом, можно проверить, является ли s палиндромом, оценивая, есть ли у самой длинной подстроки палиндрома s_1...n-2 длина - 2 с s₀ = s_n-1. В примере 7.7 приводится альтернативный метод, вызывающий только себя и использующий решение подзадачи на рисунке 1(d). Время его выполнения:

            1,                        если 0 ≤ n ≤ 1,
    T(n) =                                            
            2T(n - 1) + T(n - 2) + 1, если n > 1,

чей порядок роста - Θ((1 + √2)ⁿ) = Θ((2.41...)ⁿ).

Пример 7.7. Альтернативный метод поиска самого длинного палиндрома в строке

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def longest_palindrome_substring_alt(s):
    n = len(s)
    if n <= 1:
        return s
    else:
        s_aux_1 = longest_palindrome_substring_alt(s[1:n - 1])
        if len(s_aux_1) == n - 2 and s[0] == s[n - 1]:
            return s
        else:
            s_aux_2 = longest_palindrome_substring_alt(s[1:n])
            s_aux_3 = longest_palindrome_substring_alt(s[0:n - 1])   
            if len(s_aux_2) > len(s_aux_3):
                return s_aux_2
            else:
                return s_aux_3

Архив с файлом можно взять здесь.

Так что этот метод ещё менее эффективен, чем метод в примере 7.6, поскольку обрабатывает гораздо больше перекрывающихся идентичных подзадач.

Со следующего шага мы начнем рассматривать фракталы.

Предыдущий шаг Содержание Следующий шаг