На этом шаге мы приведем реализацию этих обходов.

При прямом (preorder) и обратном (postorder) порядках обхода двоичного дерева корневой ключ (и сам корневой узел) печатается не между рекурсивными вызовами, а до и после них соответственно. В примере 7.5 приводятся методы, осуществляющие такие обходы.

Пример 7.5. Прямой и обратный обходы двоичного дерева

1
2
3
4
5
6
7
8
9
10
11
12

def preorder_traversal(T):
    if T != []:
        print(T[0], ': ', T[1], sep='')  # печать ключа и значения     
        preorder_traversal(T[2])  # обработать левое поддерево
        preorder_traversal(T[3])  # обработать правое поддерево


def postorder_traversal(T):
    if T != []:
        postorder_traversal(T[2])  # обработать левое поддерево
        postorder_traversal(T[3])  # обработать правое поддерево
        print(T[0], ': ', T[1], sep='')  # печать ключа и значения

Архив с файлом можно взять здесь.

Отметим, что процедура прямого обхода печатает ключ корневого узла всего дерева или любого из его поддеревьев перед вызовом метода с непустым деревом. Поэтому прямой обход задаёт порядок, при котором рекурсивные вызовы только предполагается выполнить (один для каждого узла двоичного дерева). В частности, метод preorder_ traversal для списка (5.1) даст следующий результат:

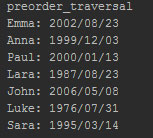
Рис.1. Результат выполнения метода preorder_ traversal

Напротив, последовательность ключей обратного обхода отражает порядок, при котором рекурсивные вызовы уже выполнены. В частности, обратный обход двоичного дерева дней рождения даст следующую последовательность ключей (рисунок 2):

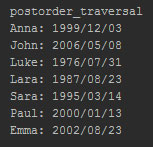
Рис.2. Результат выполнения метода postorder_traversal

Заметьте, что ключ корня исходного дерева ('Emma') оказывается последним, поскольку вызов метода для дерева в целом является последним, завершающим.

На следующем шаге мы рассмотрим самый длинный палиндром в строке.

Предыдущий шаг Содержание Следующий шаг