На этом шаге мы рассмотрим рекурсивный алгоритм построения снежинки Коха.

    Снежинка Коха - это фрактальный рисунок, состоящий из множества прямых отрезков и называемый "кривой Коха". Эта кривая создаётся многократным применением к отрезкам прямой следующего правила. Исходный отрезок прямой длины L (см. рисунок 1) делится на 3 равных отрезка длины L/3, и средний из них "ломается" - заменяется двумя сторонами равностороннего треугольника с длиной стороны L/3 (шаг 1).

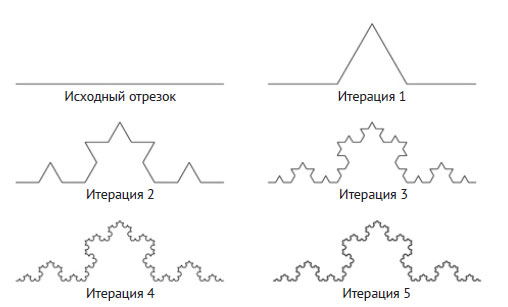
Рис.1. Фрактальная кривая Коха

    Таким образом, новая кривая имеет длину 4L/3. Фрактал Коха формируется применением этого правила к каждому отрезку кривой. Так, например, кривая на шаге 2 получается применением этого правила к каждому из четырёх прямых отрезков шага 1. Новая кривая состоит уже из 16 отрезков длиной L/9 каждый, а её полная длина - (4/3)²L. Понятно, что после n итераций длина кривой будет равна (4/3)ⁿL, которая вместе с n стремится к бесконечности.

    Снежинка Коха создаётся применением этого правила к каждой из трёх сторон равностороннего треугольника с генерацией трёх кривых Коха. На рисунке 2 показано несколько первых шагов создания снежинки Коха.

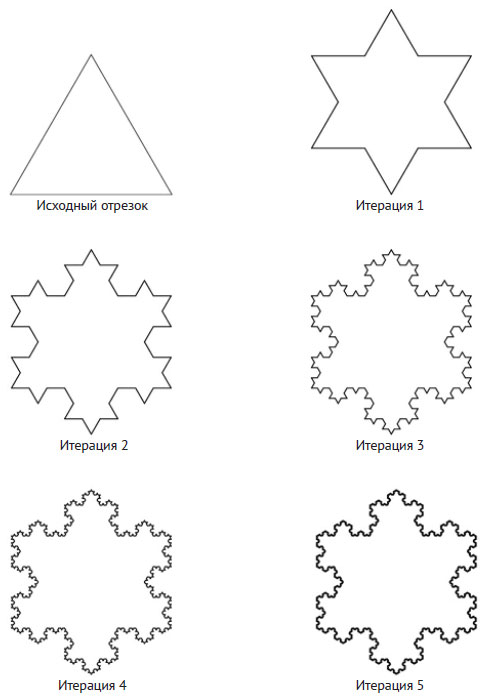
Рис.2. Фрактальная снежинка Коха

    С вычислительной точки зрения задача генерации кривой Коха определяется тремя входными параметрами - двумя концевыми точками p и q (координатами на плоскости) исходного отрезка прямой и количеством итераций n. Понятно, что размер задачи - n, так как он определяет количество шагов для генерации рекурсивного изображения. Начальное условие - это простейший случай n = 0, когда алгоритм просто чертит линию от p до q.

    На рисунке 3 показана декомпозиция задачи, которую мы будем использовать для вывода рекурсивного условия. Отметим, что кривая Коха после n шагов состоит из четырех более простых кривых Коха, созданных на шаге n - 1.

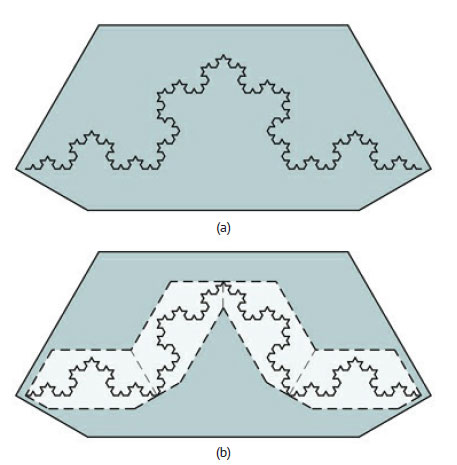
Рис.3. Декомпозиция кривой Коха

    Основная математическая задача состоит в том, чтобы определить концевые точки каждой меньшей кривой Коха. На рисунке 4 показан один из способов их получения с использованием векторов.

Рис.4. Новые концевые точки на очередном шаге построения кривой Коха

    Во-первых, отрезок прямой от точки p до точки q можно считать вектором на плоскости (a). Кроме того, пусть v = q - p, тогда концевые точки на исходном отрезке находятся на расстоянии одной и двух третей его длины от р, то есть p + v/3 и p + 2v/3 соответственно (b), (с). Последнюю концевую точку х, лежащую вне отрезка (p, q), можно получить как сумму p + v/3 + R_60°v/3, где

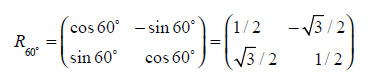
    Для генерации кривых Коха пример 7.8 использует пакеты NumPy и Matplotlib. Начальное условие просто чертит отрезок прямой от p до q. Рекурсивное условие вызывает метод четырежды с соответствующими концевыми точками, уменьшая количество итераций на 1. Снежинку Коха можно получить, генерируя кривые Коха для трёх начальных отрезков, которые образуют равносторонний треугольник. Наконец, отметим, что код определяет векторы-столбцы согласно большинству источников, где векторы соответствуют векторам-столбцам.

import math
import numpy as np
import matplotlib.pyplot as plt


def koch_curve(p, q, n):
    if n == 0:  # Базовый случай - это просто отрезок прямой
        plt.plot([p[0, 0], q[0, 0]], [p[1, 0], q[1, 0]], 'k-')    
    else:

        v = q - p
        koch_curve(p, p + v / 3, n - 1)

        R_60 = np.matrix([[math.cos(math.pi / 3),
                           -math.sin(math.pi / 3)],
                          [math.sin(math.pi / 3),
                           math.cos(math.pi / 3)]])

        x = p + v / 3 + R_60 * v / 3
        koch_curve(p + v / 3, x, n - 1)

        koch_curve(x, p + 2 * v / 3, n - 1)

        koch_curve(p + 2 * v / 3, q, n - 1)


def koch_snowflake(n):
    p = np.array([[0], [0]])
    q = np.array([[1], [0]])
    r = np.array([[0.5], [math.sqrt(3) / 2]])
    koch_curve(p, r, n)
    koch_curve(r, q, n)
    koch_curve(q, p, n)


fig = plt.figure()
fig.patch.set_facecolor('white')
koch_snowflake(3)
plt.axis('equal')
plt.axis('off')
plt.show()

    Результат работы приложения приведен на рисунке 5.

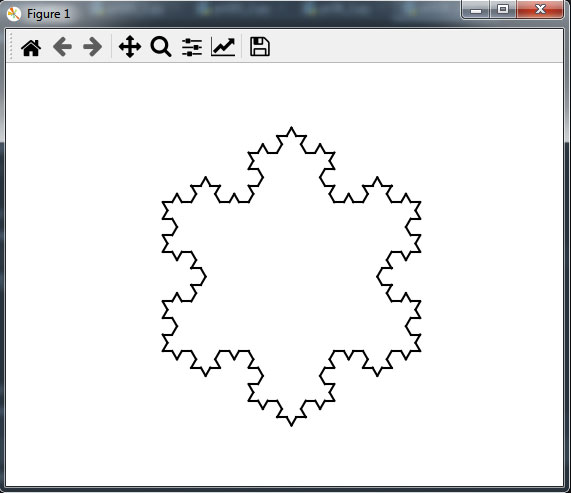
Рис.5. Результат работы приложения

    На следующем шаге мы рассмотрим ковёр Серпиньского.

Предыдущий шаг Содержание Следующий шаг