На этом шаге мы рассмотрим алгоритм рекурсивного построения ковра Серпиньского.

Ковёр Серпиньского - второй классический фрактал, который формируется следующим образом. Заданный пустой квадрат с длиной стороны s делится на 9 равных квадратов с длиной стороны s/3, и центральный из них закрашивается (то есть заполняется некоторым цветом), как показано на рисунке 1 (шаг 1).

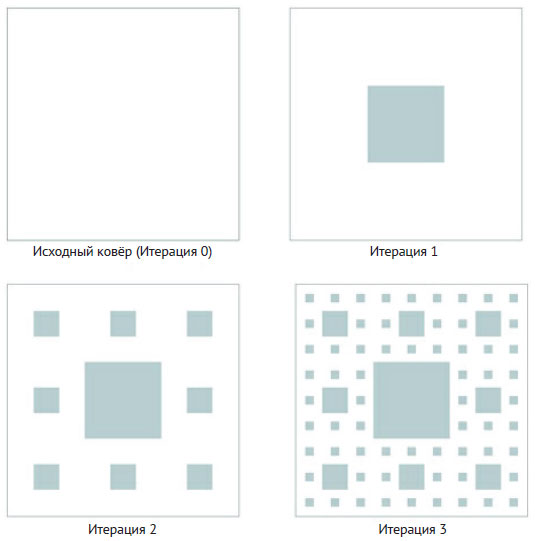
Рис.1. Ковёр Серпиньского после 0-го, 1-го, 2-го и 3-го шагов

Затем то же самое проделывается с восемью меньшими пустыми квадратами, окружающими центральный, что приводит к картинке на рисунке 1 (шаг 2). Этот процесс можно повторять и дальше вплоть до некоторого n-го шага. Добавим только, что квадратные рамки вокруг фрактальных картинок на рисунке 1 служат лишь для удобства их восприятия, но не являются частью фрактала.

Входами задачи могут быть координаты начальной точки р на плоскости - центра пустого исходного квадрата (без краёв), длина его стороны s и количество желаемых шагов n. Ясно, что размер задачи определяется n, а начальное условие возникает при n = 0, что не требует никаких действий.

На рисунке 2показана декомпозиция задачи для общего рекурсивного условия, когда квадрат делится на девять подквадратов со сторонами s/3, а в примере 7.9 приведена возможная реализация метода.

Рис.2. Декомпозиция ковра Серпиньского

Если n > 0, то прежде всего рисуется квадрат с центром в точке р. Его левый нижний угол расположен в точке р - [s/6, s/6], а длина его стороны - s/3 (эти значения используются методом Rectangle из Matplotlib). Затем на шаге n - 1 на оставшихся восьми меньших квадратах рекурсивно рисуются восемь ковров Серпиньского размером s/3. Координаты центров этих квадратов - р + s/3, 0, или -s/3 по каждой размерности. Наконец, код в строках 39-41 просто рисует границы пустого исходного квадрата.

Пример 7.9. Генерация ковра Серпиньского

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle


def sierpinski_carpet(ax, p, n, size):
    if n > 0:
        ax.add_patch(Rectangle((p[0, 0] - size / 6,
                                p[1, 0] - size / 6),
                               size / 3, size / 3,
                               facecolor=(0.5, 0.5, 0.5),    
                               linewidth=0))

        q = np.array([[-size / 3], [-size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)
        q = np.array([[-size / 3], [0]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)
        q = np.array([[-size / 3], [size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)

        q = np.array([[0], [-size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)
        q = np.array([[0], [size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)

        q = np.array([[size / 3], [-size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)
        q = np.array([[size / 3], [0]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)
        q = np.array([[size / 3], [size / 3]])
        sierpinski_carpet(ax, p + q, n - 1, size / 3)


fig = plt.figure()
fig.patch.set_facecolor('white')
ax = plt.gca()
p = np.array([[0], [0]])
sierpinski_carpet(ax, p, 4, 1)
ax.add_patch(Rectangle((-1 / 2, -1 / 2), 1, 1,
                       fill=False, edgecolor=(0, 0, 0),
                       linewidth=0.5))
plt.axis('equal')
plt.axis('off')
plt.show()

Архив с файлом можно взять здесь.

Результат работы приложения приведен на рисунке 3.

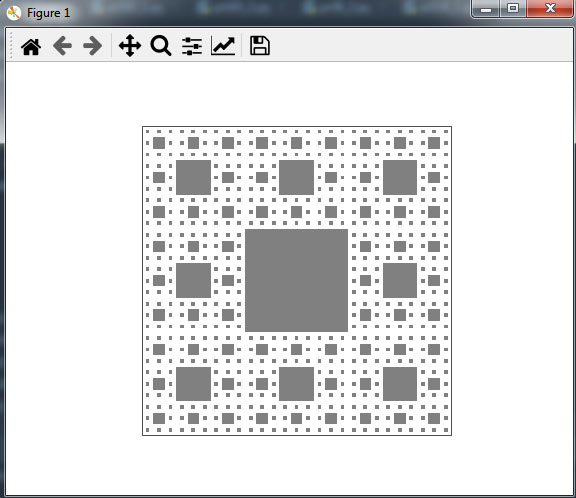
Рис.3. Результат работы приложения

На следующем шаге мы приведем примеры решений нескольких задач.

Предыдущий шаг Содержание Следующий шаг