На этом шаге мы рассмотрим особенности реализации рекурсивного способа вычисления количества перестановок.
Под перестановкой множества элементов понимается определённая последовательность этих элементов (или действие по изменению порядка следования элементов в заданной последовательности). На этом шаге мы разберём перестановки "без повторений", когда все их элементы различны. В частности, рассмотрим задачу подсчета общего количества возможных перестановок из n различных элементов. Для простоты предположим, что эти n элементов - целые числа 1, 2, ..., n, а перестановка - упорядоченный список этих элементов. Для n = 4 существует 24 различные перестановки, представленные списками на рисунке 1.
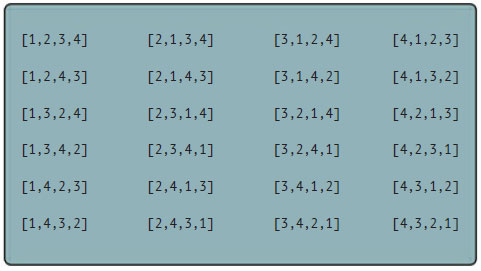
Рис.1. Возможные перестановки (списки) первых четырех положительных целых чисел
Для определения математической рекурсивной функции, обеспечивающей результат для заданного n, можно, как обычно, следовать схеме, приведенной на 20 шаге. Для задач подсчёта их размер связан с общим числом складываемых элементов. Размер данной задачи - это просто n, поскольку число перестановок растет, как функция от n. Тривиальное начальное условие выполняется при n = 1, когда получается всего одна перестановка единственного элемента. Кроме этого, можно рассмотреть случай, когда n = 0. Хотя может показаться, что результатом будет 0 перестановок, математики ради удобства считают, что число перестановок в этом случае равно 1. Например, если перестановке соответствует список, то можно считать, что при n = 0 получается один список - пустой.
Для вывода рекурсивного условия можно разбить результат на n подзадач размера n - 1, как показано на рисунке 2, где каждая из подзадач подсчитывает возможные перестановки в разных подмножествах.
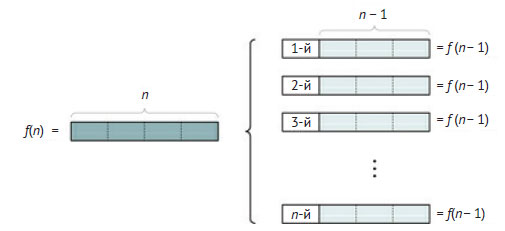
Рис.2. Декомпозиция задачи подсчёта возможных перестановок f(n) для n различных элементов
Пусть f(n) - функция, которая вычисляет количество возможных перестановок n различных элементов. Если мы зафиксировали элемент в первой позиции перестановки, то нам нужно посчитать количество возможных перестановок для оставшихся n - 1 элементов. По нашему определению, это количество равно f(n - 1), которое, по принципу индукции, мы считаем известным. Наконец, поскольку в первой позиции перестановки может оказаться каждый из n элементов, f(n) определяется как f(n - 1), сложенное с собой n раз, что, очевидно, можно записать как n * f(n - 1). Таким образом, вместе с начальными условиями определение функции будет
1, если n = 0,
T(n) =
n * f(n - 1), если n > 1,

Рис.3. Декомпозиция возможных перестановок первых четырёх положительных целых чисел
Наконец, нетрудно видеть, что нужный результат даёт функция вычисления факториала, поскольку существует ровно n способов выбрать первый элемент перестановки, n - 1 способов выбрать второй (зафиксировав первый), n - 2 способов выбрать третий и т. д. Это, естественно, приводит к n! = n * (n - 1) * (n - 2) * ... * 1 различным перестановкам. Однако такое рассуждение ближе к итерационному, тогда как представленное выше рекурсивное решение опирается на индукцию и декомпозицию задачи.
На следующем шаге мы рассмотрим размещения с повторениями.
