На этом шаге мы рассмотрим особенности рекурсивного решения этой задачи.

    Рассмотрим некоторое множество из n элементов. В комбинаторике размещением из n элементов множества по k элементов называется последовательность из k ≤ n элементов, в которой имеет значение порядок следования элементов. Если для записи размещений использовать списки, то [a₁, a₅, a₈] и [a₈, a₅, a₁] - это два разных размещения по 3 элемента на множестве {a₁, a₂, ..., a₁₀}. Кроме того, если элементу разрешается появляться в последовательности не один раз, то такое размещение называется размещением "с повторениями" (например, [a₁, a₅, a₁] было бы правильным размещением). На этом шаге мы изучим именно этот вид размещения с повторениями. На рисунке 1 приведён конкретный пример, где квадратиками обозначены элементы множества, кружочками - положения элементов в размещении, а стрелками - ссылки на конкретные элементы множества, вошедшие в размещение.

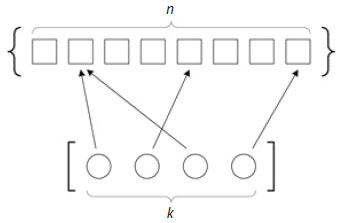
Рис.1. Пример размещения с повторениями по k элементам из n элементов множества

    Нетрудно видеть, что согласно "принципу умножения" число размещений с повторениями по k элементов на множестве из n элементов есть n^k, так как на каждом месте в размещении из k элементов может находиться (в том числе повторно) каждый из n элементов множества. Тем не менее мы выведем этот факт, используя рекурсию.

    Задача определяется параметрами k и n. Хотя задачу можно свести к меньшим подзадачам путём уменьшения k и/или n, декомпозиция будет проще, если считать размером задачи k. Тривиальное начальное условие выполняется при k = 1, когда существует ровно n различных способов выбрать один элемент из множества. Кроме того, как в задаче о перестановках, можно рассмотреть случай, когда k = 0, который можно понимать как пустое размещение.

    Для вывода рекурсивного условия можно воспользоваться схемой на рисунке 2.

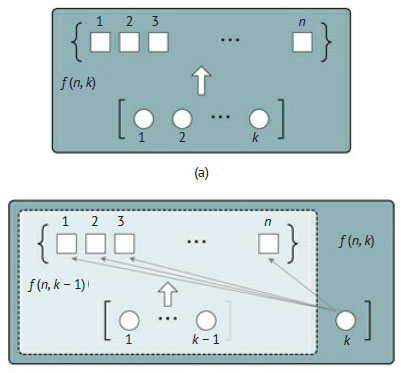
Рис.2. Декомпозиция задачи подсчёта размещений с повторениями n элементов множества в k позициях

    Исходная задача, обозначенная f(n, k), показана на рисунке 2(a), где толстая стрелка заключает в себе все возможные отношения между множеством и размещением. На рисунке 2(b) приведена подзадача с уменьшенным на 1 исходным размером, которая подсчитывает все способы размещения n элементов в k - 1 позициях. Наконец, поскольку существует n способов разместить элементы множества в последней k-й позиции, общее количество размещений будет f(n, k - 1), сложенное n раз. Таким образом, рекурсивная функция определяется как

              1,               если k = 0,
    f(n, k) =                                            
              f(n, k - 1) * n, если k > 1, 

    На следующем шаге мы рассмотрим сочетания.

Предыдущий шаг Содержание Следующий шаг