На этом шаге мы рассмотрим особенности такого решения.

Рекурсивное выражение (9.3) можно вычислить в цикле (см. пример 1.4). Решение, к которому мы хотим прийти, заменяет суммирование рекурсивной функцией (это важно, если язык программирования не поддерживает циклы).

Во-первых, взаимная рекурсия возникает только тогда, когда в исходной задаче можно выделить несколько разных задач. В данном случае, помимо функции f(n), решающей исходную задачу, мы рассмотрим ещё и решение похожей, но иной задачи. А именно пусть g(n) - количество пар детей в возрасте от 1 до n месяцев вместе с их потомками от начальной пары. С помощью этой вспомогательной функции просто определить f(n), а именно: для заданного n она подсчитывает всю семью начальной пары кроликов плюс g(n - 2), поскольку начальная пара всегда на 2 месяца старше самых старших своих детей. Таким образом, f(n) можно выразить так:

            1,            если n = 1 или n = 2,
    f(n) =                                                       (9.4)
            1 + g(n - 2), если n > 2    .

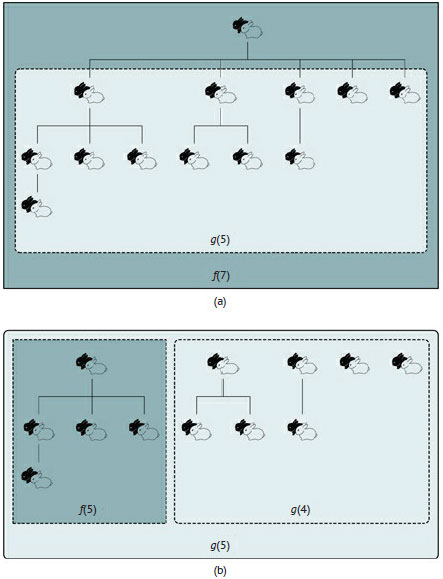
что соответствует декомпозиции на рисунке 1(a) при n = 7.

Рис.1. Декомпозиция задачи о размножении кроликов, приводящая к двум взаимно-рекурсивным функциям

Для функции g() размер задачи - n. Тривиальное начальное условие с результатом 1 выполняется при n = 1. Но можно также использовать начальное условие g(0) = 0. Вывод рекурсивного условия основан на декомпозиции, уменьшающей размер задачи на 1 (см. рисунке 1(b)). Заметим, что общее количество пар кроликов - это сумма количества пар для некоторой начальной пары спустя n месяцев f(n) и количества детей в возрасте не старше n - 1 месяцев вместе с их потомками g(n - 1). Следовательно, g(n) можно записать так:

            0,               если n = 0,
    g(n) =                                                       (9.5)
            f(n) + g(n - 1), если n > 0    .

В результате мы получили пару взаимно-рекурсивных функций, которые вызывают друг друга. Кроме того, отметим, что g(n) просто равна

            _n
            ∑ f(i)    .
            ⁱ⁼¹

Таким образом, (9.4) и (9.5) равносильны (9.3). В итоге можно без труда закодировать эти функции, как показано в примере 9.4.

Пример 9.4.Альтернативные взаимно-рекурсивные функции подсчёта популяции кроликов спустя n месяцев

1
2
3
4
5
6
7
8
9
10
11
12
13

def population_rabbits(n):
    if n <= 2:
        return 1
    else:
        return 1 + children_descendants(n - 2)    


def children_descendants(n):
    if n == 0:
        return 0
    else:
        return (population_rabbits(n) +
                children_descendants(n - 1))

Архив с файлом можно взять здесь.

На следующем шаге мы рассмотрим задачу о станциях водоочистки.

Предыдущий шаг Содержание Следующий шаг