На этом шаге мы рассмотрим особенности такого решения.

Первая приходящая на ум в связи с этой задачей декомпозиция - разбить задачу так, как показано на рисунке 1.

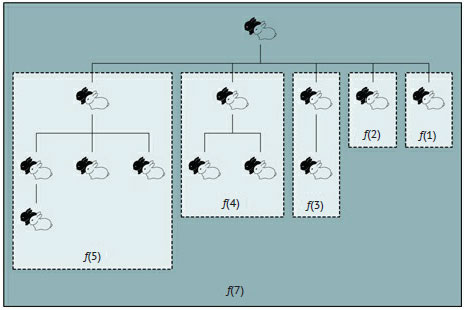
Рис.1. Конкретный пример разбиения задачи о росте популяции кроликов на подобные ей подзадачи

В этом конкретном примере задача размера 7 разбита на пять меньших задач размером от 1 до 5. Заметим, что начальная пара кроликов с третьего месяца создаёт новую пару потомков, каждая из которых уже имеет своих потомков. Каждая пара потомков вместе со своими потомками образует меньшую задачу, подобную исходной. Таким образом, в рекурсивном условии искомая функция f(n) - это пара, прожившая n месяцев плюс общее количество её потомков. Формально декомпозиция приводит к следующему определению:

            1,           если n = 1 или n = 2,
    f(n) =                                                       (9.3)
                _n-1
            1 + ∑ f(i), если n > 2    .
                ⁱ⁼¹

где используется множественная рекурсия, подобная (1.7). Более того, схема декомпозиции задачи на рисунке 1 пригодна для любого n (напомним, что f(n) = F(n), где F - функция Фибоначчи).

На следующем шаге мы рассмотрим решение со взаимной рекурсией.

Предыдущий шаг Содержание Следующий шаг