На этом шаге мы приведем рекурсивную функцию, решающую эту задачу.

Вода по каждой из соединяющих соседние города n - 1 труб может перетекать в трёх направлениях:

'N' - перетока нет,
'R' - направо и
'L' - налево.

Следовательно, сброс воды в реку можно смоделировать строкой длины n - 1, состоящей только из этих символов. Единственное ограничение, касающееся перетока воды, состоит в том, что город не имеет права направить свою воду обоим своим соседям. Таким образом, цель задачи в том, чтобы найти все строки, в которых нет подстроки "LR".

Очевидно, что размер задачи - n. Пусть f(n) представляет решение задачи. Если есть только один город, то его водоочистная станция может сбросить в реку лишь свою воду, то есть f(1) = 1. Для двух городов существует 3 варианта строки размера 1 с одним из трех символов, то есть f(2) = 3. Заметим, что если обе станции работают, они сбросят в реку только воду своих городов, а если какая-то из них не работает, она направит свою воду на соседнюю станцию.

На рисунке 1 представлена декомпозиция задачи, приводящая к алгоритму с множественной рекурсией.

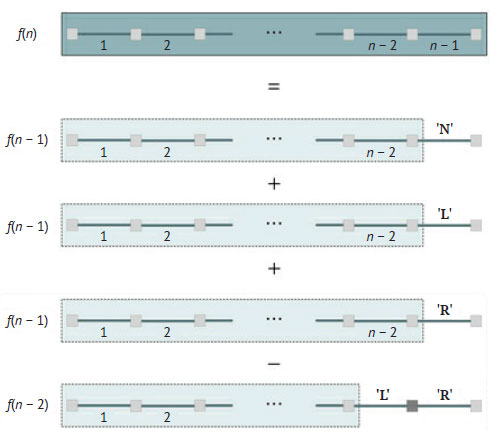
Рис.1. Декомпозиция задачи о станциях водоочистки, моделирующая переток воды между городами

Сначала общее количество возможных строк длины n - 1 втрое больше количества правильных строк длины n - 2, так как к каждой из них можно добавить один из трёх символов, что даёт слагаемое 3f(n - 1). Однако к строке с окончанием 'L' нельзя добавить 'R', поскольку тогда станция n - 1 направляла бы воду в обоих направлениях, что недопустимо. Поэтому все возможные строки длины n - 1 с окончанием "LR" необходимо исключить, а их количество равно f(n - 2). Таким образом, рекурсивное правило - f(n) = 3f(n - 1) - f(n - 2). Вместе с начальными условиями функцию можно определить как

            1,                    если n = 1,
    g(n) =  3,                    если n = 2,                  (9.6)
            3f(n - 1) - f(n - 2), если n > 2    ,

и можно легко реализовать, как показано в примере 9.5. Наконец, f(n) = F(2n), где F - функция Фибоначчи.

Пример 9.5. Функция с множественной рекурсией для решения задачи о станциях водоочистки

1
2
3
4
5
6
7

def water_multiple(n):
    if n == 1:
        return 1
    elif n == 2:
        return 3
    else:
        return 3 * water_multiple(n - 1) - water_multiple(n - 2)

Архив с файлом можно взять здесь.

На следующем шаге мы рассмотрим сброс воды в каждом городе.

Предыдущий шаг Содержание Следующий шаг