На этом шаге мы рассмотрим другой подход к решению этой задачи.

    Другой подход к решению задачи заключается в моделировании направлений передачи воды станциями. Существует 3 направления передачи воды, которые мы обозначим следующими символами:

• 'v' - сброс в реку,
• '>' - переток вправо,
• '<' - переток влево.

    Для создания алгоритма со взаимной рекурсией будем использовать три похожие, но разные задачи. Рассмотрим правильные строки из трёх символов, начинающихся (слева направо) с непустой подстроки и заканчивающихся подстрокой из n символов. В зависимости от начального символа, предшествующего подстроке длины n (подстрока слева от символа неуместна), существует 3 сценария (подзадачи), которые представлены схемами на рисунке 1 и заключаются в определении количества правильных подстрок в каждом из трёх случаев. Их решения обозначены функциями f_v(n), f_>(n) и f_<(n), где нижний индекс указывает на символ, предшествующий подстроке длины n.

Рис.1. Три сценария взаимно-рекурсивного решения задачи о станциях водоочистки

    Очевидно, что размер задач - n, а их начальные условия выполняются при n = 1. В частности, f_v(1) = f_<(1) = 2, так как существует всего два варианта ('v' и '<') для самого последнего символа. Наоборот, f_>(1) = 1, так как последняя станция очистки, получившая воду от своего соседа, должна сбросить её в реку.

    На рисунке 2 приведены декомпозиции задач.

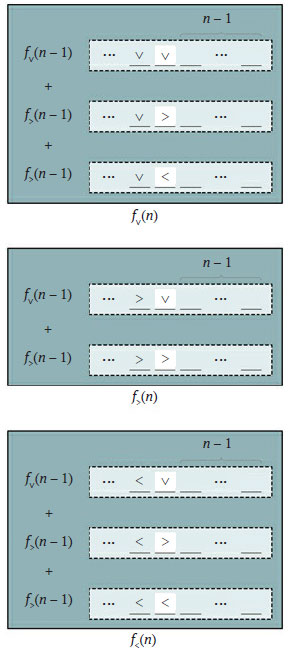
Рис.2. Декомпозиции трех подзадач для взаимно-рекурсивного решения задачи о станциях водоочистки

    Для f_v(n) и f_<(n) первый символ подстроки длины n может быть любым. Поэтому общее количество правильных строк длины n равно количеству правильных строк длины n - 1 для каждого из трёх первых символов.

    Таким образом, в правой части рекурсивного правила для обеих функций будет формула f_v(n - 1) + f_>(n - 1) + f_<(n - 1). Кроме того, поскольку их начальные условия тоже одинаковы, одинаковыми будут и сами функции. В результате мы имеем:

                     2,                                если n = 1,
    fv(n) = f<(n) =                                                     (9.7)
                     fv(n - 1) + f<(n - 1) + f>(n - 1), если n > 1    .

    Наоборот, для f_>(n) символ '<' не может быть первым в строке длины n. Поэтому в правой части её рекурсивного правила будет f_v(n - 1) + f_>(n - 1). А сама функция вместе с ее начальным условием будет такой:

            1,                    если n = 1,
    f>(n) =                                              (9.8)
            fv(n - 1) + f>(n - 1), если n > 1    .

    Итак, решение f(n) исходной задачи можно выразить двояко:

    f(n) = fv(n - 1) + f>(n - 1) = f>(n).

    Первое равенство говорит о том, что первым символом строки может быть или 'v', или '<', и в этом случае мы должны сложить число правильных строк длины n - 1, начинающихся с этого символа. Второе равенство следует из рекурсивного правила для f_>(n). Наконец, можно показать, что f_v(n) = f_<(n) = F(2n + 1), а f_>(n) = F(2n), где F - функция Фибоначчи.

    На следующем шаге мы рассмотрим циклические ханойские башни.

Предыдущий шаг Содержание Следующий шаг