На этом шаге мы рассмотрим работу этой функции.
До рассмотрения прочих рекурсивных условий мы остановимся сначала на более простом лексическом анализе. Следующее рекурсивное условие выполняется, если первый символ входной строки (s0) является цифрой (строка 36 примера 9.7), которая, естественно, относится к некоторому числу. В этом случае алгоритм должен выполнить разные действия в зависимости от следующего символа (s1) или первой лексемы остальной части строки (s1...n-1).
Во-первых, если s1 - пробел, то s0 - лексема. Значит, метод должен вернуть список, первый элемент которого - s0, плюс список лексем остатка строки s2...n-1. Это можно представить следующей схемой:
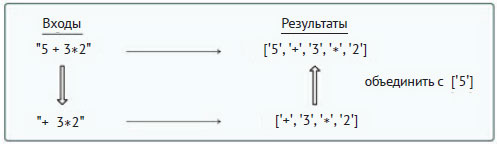
В противном случае метод посредством рекурсивного вызова ищет лексемы в s1 и сохраняет их в списке t (строка 40 примера 9.7). Если этот список пуст, то метод просто вернёт лексему, соответствующую s0 (строка 42 примера 9.7). Иначе последующее действие будет зависеть от того, является или нет первая лексема s1 числом. Рассмотрим следующую частную схему:
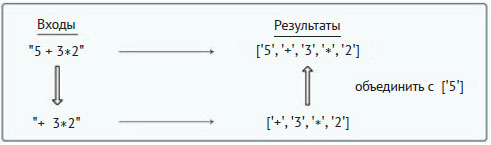
Поскольку первая лексема t ('+') не является числом, алгоритм должен присоединить список, содержащий s0, к списку t (строка 48 примера 9.7).
Иначе, если первая лексема t - число, метод должен добавить символ s0 к первой лексеме (строки 45 и 46 примера 9.7). Следующая схема иллюстрирует это:

Заметьте, что таким образом алгоритм собирает из отдельных цифр числовую лексему.
Наконец, есть еще два рекурсивных условия, когда первый элемент строки не является цифрой. Поскольку функция уже проверила, что символ не является пропуском (строка 34 примера 9.7), он может быть только лексемой - операцией или круглой скобкой. Таким образом, метод добавит эту лексему к результату решения задачи для s1...n-1. Однако если символ s0 является левой круглой скобкой, то первой лексемой оставшейся подстроки может быть унарный минус, и в этом случае метод должен вызвать функцию tokenize_unary() (строка 51 примера 9.7). В любом другом случае унарный минус не может быть первой лексемой, и метод может вызвать просто сам себя (строка 53 примера 9.7).
На следующем шаге мы рассмотрим функцию tokenize_unary().
