На этом шаге мы опишем работу этой функции.

    В примере 9.9 приведена функция, обрабатывающая выражение (E).

def expression(tokens):
    if tokens == []:
        raise SyntaxError('Syntax error')
    else:
        par_counter = 0
        i = len(tokens) - 1
        while i > 0 and ((tokens[i] != '+' and tokens[i] != '-')    
                         or par_counter > 0):
            if tokens[i] == ')':
                par_counter = par_counter + 1
            if tokens[i] == '(':
                par_counter = par_counter - 1

            i = i - 1

        if i == 0:
            if tokens[0] == '-':
                return -inverted_term(tokens[1:])
            else:
                return term(tokens)
        else:
            e = expression(tokens[0:i])
            t = term(tokens[i + 1:])
            if tokens[i] == '+':
                return e + t
            else:
                return e - t

    Сначала все функции синтаксического анализатора на основе рекурсивного спуска проверяют список лексем на пустоту, сообщая при этом о синтаксической ошибке. В противном случае метод выбирает подходящее порождающее правило в предположении, что входной список лексем представляет собой выражение. Варианты выбора приведены на рисунке 1.

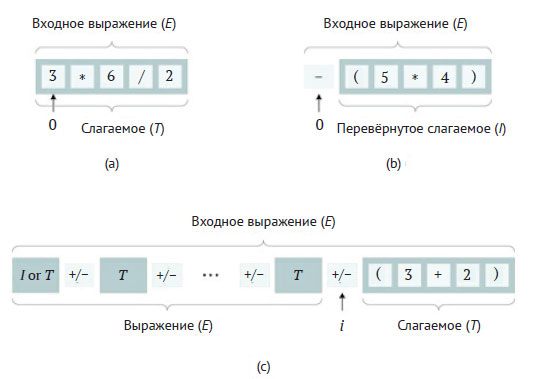
Рис.1. Возможные декомпозиции выражения

    С одной стороны, выражение может быть простым (T) или "перевёрнутым" (I) слагаемым (варианты (a) и (b) на рисунке). С другой стороны, если выражение содержит более одного слагаемого, то оно разбивается на меньшее подвыражение (E) плюс/минус слагаемое (T), как в случае (c).

    Для распознавания этих вариантов функция использует цикл while (строки 7-14), который, начиная с конца списка (то есть справа налево), ищет первую бинарную операцию плюс или минус, находящуюся вне любых круглых скобок. Метод подсчитывает левые и правые круглые скобки в переменной-сумматоре par_counter. После выхода из цикла переменная i (i на рисунке 1(c)) будет содержать либо индекс найденной лексемы '+' или '-', либо 0, если её нет (то есть выражение состоит из одного слагаемого). В этом случае может быть два варианта. Если первой лексемой входного списка является '-', то это - "перевёрнутое" слагаемое (I), и в этом случае функция должна вернуть результат метода inverted_term(tokens[1:]) с входным списком лексем без первой лексемы '-' (строка 18). В противном случае это будет обычное слагаемое (T), и функция может вызвать term(tokens) в строке 20. Если же i больше 0, то tokens[i] будет бинарной операцией ('+' или '-'). В этом случае функция вычисляет выражение слева от этой лексемы, сохраняя результат в е, и слагаемое справа от неё, сохраняя результат в t. После чего метод в зависимости от операции token[i] возвращает сумму или разность е и t, которые, очевидно, вычисляются взаимно-рекурсивными вызовами функций.

    На следующем шаге мы рассмотрим функцию term().

Предыдущий шаг Содержание Следующий шаг