На этом шаге мы рассмотрим еще один пример построения и использования дерева рекурсии.
Рассмотрим ещё одну функцию - функцию Фибоначчи из примера 1.3. На рисунке 1 приведено её дерево рекурсии для вычисления 6-го числа Фибоначчи.
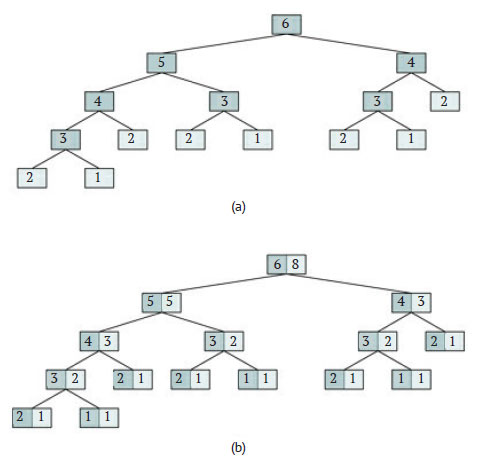
Рис.1. Деревья рекурсии (a) и активации (b) для fibonacci(6)
Оно сложнее из-за множественной рекурсии. В частности, оно - двоичное, так как рекурсивное условие содержит два рекурсивных вызова. Дополнительно на рисунке 1(b) приведено соответствующее дерево активации. Результат метода - количество листьев в этих деревьях, так как по определению метод возвращает 1 в начальном условии и сумму двух вызовов в рекурсивном условии. Таким образом, алгоритм просто подсчитывает, сколько раз он достигает начального условия.
Наконец, если метод - это процедура, не возвращающая значения, то в дерево рекурсии рядом со стрелками, указывающими последовательность вызовов, можно включить дополнительную информацию о действиях этой процедуры. Например, рисунки 1 и 2 154 шага похожи на деревья рекурсии (где каждый узел включает ещё и исходный текст), но отображают ещё и состояние экрана до и после вызова.
Деревья рекурсии можно генерировать и для других типов рекурсии. Во-первых, взаимно-рекурсивные методы тоже могут порождать деревья рекурсии с линейной структурой. Самый простой пример - методы из примера 9.1, определяющие чётность неотрицательного целого числа. На рисунке 2 приведено дерево активации для is_even(5), чей результат - False.
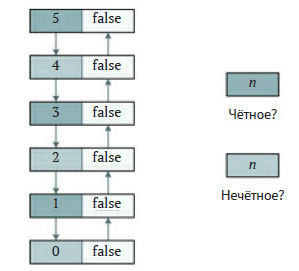
Рис.2. Дерево активации для взаимно-рекурсивных функций из примера 9.1
Обратите внимание, что методы относятся к хвостовой рекурсии. Таким образом, логическое значение, полученное в начальном условии, просто "всплывает" вверх по дереву в неизменном виде как результат вызовов функций.
Деревья рекурсии могут быть ещё сложнее, если алгоритм включает множественную рекурсию. На рисунке 3 приводится пример дерева рекурсии для взаимно-рекурсивных функций (1.17) и (1.18), где корневой узел соответствует A(6).
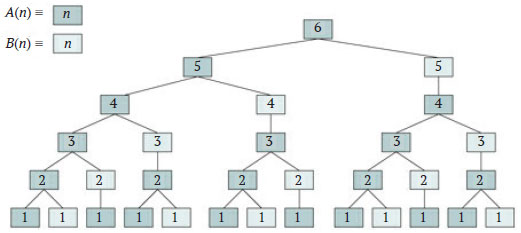
Рис.3. Дерево рекурсии для взаимно-рекурсивных функций (1.17) и (1.18)
Создание дерева рекурсии для вложенных рекурсивных функций ещё сложнее, так как для определения параметров функции необходимо знать результаты всех рекурсивных вызовов. Таким образом, для вложенных рекурсивных функций больше подходят деревья активации, чем обычные деревья рекурсии. На рисунке 4(a) приведено дерево активации вызова f(6, 0) функции (1.19), а на рисунке 4(b) - детализация вложенных рекурсивных вызовов.
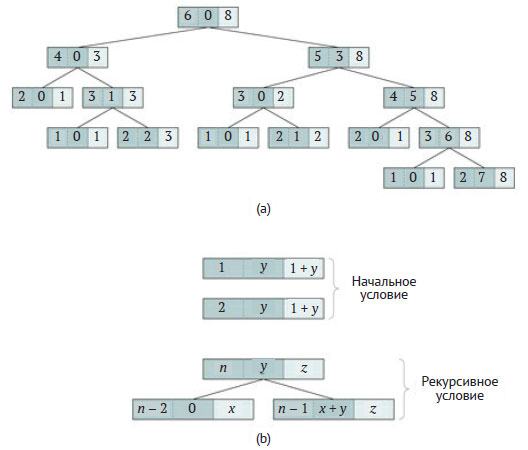
Рис.4. Дерево активации вложенной рекурсивной функции (1.19)
Левое поддерево отвечает вызову f(4, 0), возвращающему некоторое значение х. Правое поддерево, отвечающее вызову f(5, 0 + х), невозможно детализировать, пока не получено конкретное значение х - результат вычисления f(4, 0) (левое поддерево корневого узла). В данном случае f(4, 0) = х = 3, поэтому правое поддерево корневого узла соответствует вызову f(5, 3).
На следующем шаге мы рассмотрим анализ времени выполнения.
