На этом шаге мы рассмотрим особенности такого анализа.

    Число узлов (то есть рекурсивных вызовов) дерева рекурсии позволяет также оценить вычислительную сложность рекурсивного алгоритма. Если дерево линейно, то понятно, что время выполнения метода прямо пропорционально высоте дерева (стоимость узла умножается на высоту дерева). Но можно также определить количество узлов и для нелинейного дерева. Например, следующая функция определяет количество рекурсивных вызовов в методе Фибоначчи:

            1,                       если n = 1,
    Q(n) =  1,                       если n = 2,                  
            1 + Q(n - 1) + Q(n - 2), если n ≥ 3    ,

    Она похожа на саму функцию Фибоначчи. Но, помимо подсчета листьев дерева рекурсии, она добавляет единицу для рекурсивного условия, чтобы учесть также и его внутренние рекурсивные вызовы. В этом случае можно доказать, что Q(n) = 2F(n) - 1, где F(n) - n-е число Фибоначчи. Согласно (3.37), количество (приблизительное) вызовов имеет значение порядка 1,618ⁿ. Стоит заметить, что количество узлов полного двоичного дерева высоты n можно оценить как 2ⁿ. Двоичное дерево рекурсии для чисел Фибоначчи содержит несколько меньше узлов, поскольку оно - неполное. Таким образом, вполне объяснимо, что основание соответствующей экспоненты (1,618...) меньше двух.

    Кроме того, деревья рекурсии могут использоваться для оценки времени выполнения алгоритмов типа "разделяй и властвуй" с помощью подхода, называемого "метод дерева", который связан с методом расширения и основной теоремой. Идея заключается в формировании другого дерева рекурсии, узлы которого включают стоимость операций, выполняемых в пределах вызова рекурсивного метода, за исключением предстоящих вызовов. На рисунке 1 приводится такое дерево для рекуррентного соотношения T(n) = 2T(n/2) + n².

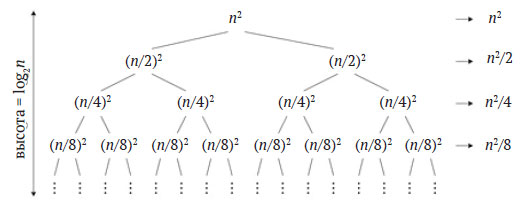
Рис.1. Дерево рекурсии для рекуррентного соотношения T(n) = 2T(n/2) + n²

    Первый вызов метода требует n² операций плюс стоимость 2T(n/2) будущих вызовов. Таким образом, первый узел просто содержит n². Узлы второго уровня дерева содержат количество операций, соответствующих T(n/2), то есть (n/2)² = n²/4. Поскольку на этом уровне - два узла, общая его стоимость - n²/2. То же рассуждение применимо и для каждого из последующих уровней, суммарная стоимость которых указана на рисунке справа от соответствующего уровня, а их сумма даст в итоге стоимость алгоритма. Если предположить, что n - степень двух и начальное условие выполняется при n = 1, то высота дерева будет log₂n. В этом примере, предположив, что T(1) = 1 (последний уровень будет состоять из n слагаемых, равных 1) - окончательное нерекурсивное выражение, рекуррентное соотношение можно будет выразить так:

         log2n            
   T(n) = ∑ 1 / 2i = n2(2 - 1 / n) = 2n2 - n.
          i=0            

    На следующем шаге мы рассмотрим программный стек.

Предыдущий шаг Содержание Следующий шаг