На этом шаге мы разберемся с этим понятием.
Требования к памяти рекурсивного алгоритма зависят от наибольшего числа, скажем, h стековых кадров, помещенных в программный стек в произвольный момент вычислений. Эту величину можно также понимать как высоту дерева рекурсии. Естественно, для линейных или хвостовых рекурсивных методов h - это просто число узлов дерева рекурсии, поскольку оно линейно. В предположении, что каждый вызов рекурсивного метода требует одинакового объёма памяти М (это не всегда так), полный объём необходимой алгоритму памяти был бы М * h, поскольку в какой-то момент в программном стеке окажется h стековых кадров некоторого метода. Например, каждый стековый кадр функции sum_first_naturals() требует постоянного объёма памяти c (то есть пространства памяти порядка Θ(1)), поскольку он хранит входной параметр и фиксированное количество информации нижнего уровня. Кроме того, так как высота дерева рекурсии - n, то полный объём необходимой памяти - c * n, и мы можем заключить, что алгоритм требует пространства памяти порядка Θ(n).
Для алгоритмов с нелинейным деревом рекурсии важно понимать, что необходимая рекурсивному алгоритму память - это высота дерева рекурсии, а не количество его узлов. Рассмотрим дерево рекурсии для функции fibonacci() на рисунке 1(a), 156 шага.
Количество его узлов - показательная функция от его высоты n, но его высота - просто n - 1, и именно она определяет потребность метода в памяти. Это видно из анализа различных состояний программного стека при выполнении fibonacci(5), как показано на рисунке 1.
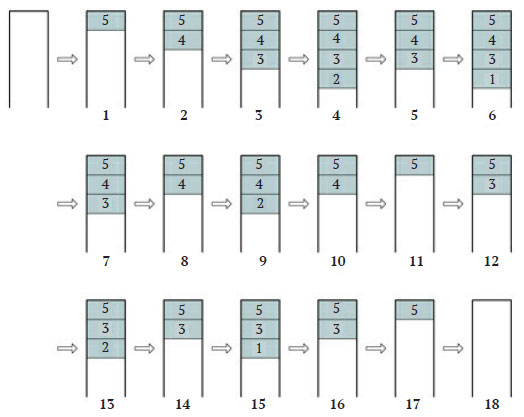
Рис.1. Выделение стековых кадров для fibonacci(5)
Так как по завершении метода стековые кадры удаляются из стека, их максимальное количество равно 4 (шаги 4 и 6). В итоге, поскольку каждый вызов требует одинакового объёма памяти для своих данных, пространственная сложность вычислений для этого алгоритма линейна относительно n.
Так как рекурсия реализуется посредством программного стека, она всегда требует, по крайней мере, h блоков памяти (то есть Ω(h)). В этом соотношении рекурсивные алгоритмы, вообще говоря, используют больше памяти, чем их итерационные версии. Например, основные итерационные алгоритмы вычисления суммы первых положительных целых чисел или чисел Фибоначчи используют постоянный объём памяти, тогда как рекурсивные версии обязательно требуют порядка n блоков памяти. Кроме этого, к дополнительным вычислительным расходам приводят стековые операции вталкивания и выталкивания. Таким образом, среди алгоритмов с одинаковой временн0й сложностью итерационные, вообще говоря, будут (несколько) эффективнее, чем рекурсивные.
На следующем шаге мы рассмотрим ошибки предельной глубины рекурсии и переполнения стека.
