На этом шаге мы рассмотрим еще один способ решения задачи о нахождении самого длинного палиндрома в заданной строке.

    Динамическое программирование - парадигма проектирования алгоритмов, применяемая для решения задач оптимизации, которые можно разбить рекурсивно на меньшие подзадачи так, что разбиение приводит к перекрывающимся подзадачам. Метод может быть нисходящим (сверху вниз) с применением рекурсии и мемоизации. Но более общий подход заключается в применении восходящей (снизу вверх) стратегии. Суть её в том, чтобы реализовать восходящий итерационный алгоритм, который заполняет поисковую таблицу (такую же, как в рекурсивном алгоритме с мемоизацией) снизу вверх, начиная с простейших экземпляров задачи, и последовательно сохраняет получаемые результаты, которые позволят нам решить исходную задачу.

    Даже при том, что восходящий подход является итерационным, рекурсивное решение даёт представление о том, как следует заполнять поисковую таблицу. В частности, аналитики могут построить граф зависимости (dependency graph), называемый также "графом подзадач", указывающий на зависимости между различными подзадачами (то есть вызовами методов), которые необходимо решить с помощью рекурсивного алгоритма. Безусловно, этот граф - ориентированный, где каждый узел представляет собой конкретную подзадачу, а рёбра - зависимости между ними. Будем считать, что если подзадача A требует решения (зависима от) подзадачи B, то соединяющее их ребро будет направлено от A к B. На рисунке 1 приведён граф зависимости для рекурсивного алгоритма на базе рекуррентного соотношения F(n) = F(n - 1) + F(n - 2) для F(6) и начальных условий F(2) и F(1).

Рис.1. Граф зависимости для F(n) = F(n - 1) + F(n - 2)

    Обратите внимание на зависимость узлов n от узлов n - 1 и n - 2. Теперь для реализации решающего задачу итерационного алгоритма граф зависимости нужно проанализировать. Очевидно, что для чисел Фибоначчи алгоритм может получить результат за n шагов при наличии сохранённых решений подзадач F(1), F(2), ..., F(n - 1). Более того, из графа зависимости видно, что нет необходимости в списке длины n для хранения всех промежуточных результатов, поскольку на каждом шаге i нам нужны только два значения - F(i - 1) и F(i - 2), которые можно хранить в двух переменных.

    Что касается задачи о самой длинной подстроке-палиндроме, то на рисунке 2 приводится граф зависимости, относящийся к примеру 10.6, для исходной входной строки из пяти символов.

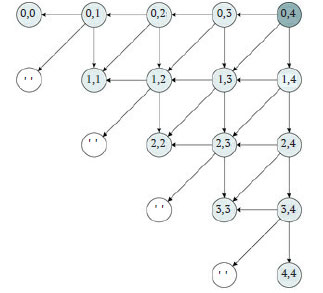
Рис.2. Граф зависимости для примера 10.6, решающего задачу о самой длинной подстроке-палиндроме

    В его узлах указаны только нижний и верхний индексы i и j (если i > j, то результатом является пустая строка, а сам узел помечен как ''). Заметьте, что узел (i, j) зависит лишь от решений для пар (i + 1, j), (i, j - 1) и (i + 1, j - 1), что следует из декомпозиции задачи. Каждый узел (i, j) связан с разными подзадачами, поэтому решение исходной задачи может быть получено только по завершении вызова, связанного с (затемнённым) узлом (0, n - 1).

    Если промежуточные результаты сохраняются в некоторой матрице L, то из графа зависимости на рисунке 2 следует, что L_i,j, связанный с узлом (i, j), может быть получен после вычисления и сохранения L_i+1,j, L_i,j-1 и L_i+1,j-1. Таким образом, граф зависимости задаёт порядок или направление (к верхнему правому углу), в котором нужно решать подзадачи и сохранять их решения. В частности, можно разработать алгоритм, который начинается с решения подзадач, расположенных на главной диагонали, с узлами (i, i) для i = 0, ..., n - 1. Затем на следующей диагонали с узлами (i, i + 1) для i = 0, ..., n - 2 и т. д. до достижения узла (0, n - 1). В примере 10.7 приведена возможная итерационная реализация алгоритма.

def lps_dynamic_programming(s):
    n = len(s)
    L = [['' for i in range(n)] for j in range(n)]

    for i in range(n):
        L[i][i] = s[i]

    k = 1
    while k < n:
        i = 0
        j = k
        while j < n:
            if (len(L[i + 1][j - 1]) == j - i - 1
                    and s[i] == s[j]):
                L[i][j] = s[i:j + 1]
            elif len(L[i][j - 1]) >= len(L[i + 1][j]):  
                L[i][j] = L[i][j - 1]
            else:
                L[i][j] = L[i + 1][j]

            i = i + 1
            j = j + 1

        k = k + 1
    return L[0][n - 1]

    Заметьте, что он решает подзадачи снизу вверх, начиная с меньших экземпляров, пока не вернёт решение всей исходной задачи. В частности, сначала он заполняет матрицу L пустыми строками (строка 3), а также сохраняет s_i в L_i,i для i = 0, ..., n - 1 (строки 5 и 6). Два следующих цикла последовательно, диагональ за диагональю, заполняют матрицу L, пока не достигнут верхнего правого узла графа зависимости. Строки 13-15 проверяют, что подстрока s_i,j является палиндромом, и, если это так, сохраняют ее. В противном случае следующие четыре строки сохраняют в L_i,j самую длинную из подстрок L_i+1,j и L_i,j-1 На рисунке 3 приведено состояние матрицы L по завершении метода со всеми решениями подзадач для исходной входной строки s = 'bcaac'. Алгоритм работает за время Θ(n²), так как создаёт квадратную матрицу L, каждый элемент которой требует времени Θ(1) (можно разработать более эффективные алгоритмы, не использующие матрицу).

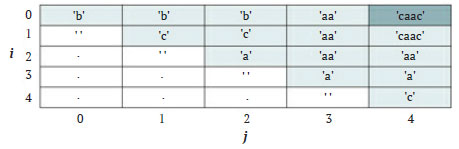
Рис.3. Матрица L по завершении метода из примера 10.7 для s = 'bcaac'

    На следующем шаге мы приведем решения нескольких задач.

Предыдущий шаг Содержание Следующий шаг