На этом шаге мы рассмотрим пример использования мемоизации.

    Некоторые рекурсивные алгоритмы несколько раз выполняют одни и те же рекурсивные вызовы (см. 116 шаг). Другими словами, им приходится неоднократно решать одинаковые перекрывающиеся подзадачи. Мемоизация - это подход, позволяющий избежать повторных вычислений при решении таких подзадач и тем самым существенно ускорить алгоритмы. Суть подхода заключается в сохранении результатов рекурсивных вызовов в поисковых таблицах. В частности, до рекурсивного вызова метод проверяет, был ли такой вызов ранее и сохранён ли его результат в таблице. Если это так, то алгоритм вместо повторного рекурсивного вызова просто возвращает его ранее вычисленный и сохранённый в таблице результат. Если же результат не был вычислен, алгоритм продолжает работу, как обычно, вызывая рекурсивный метод.

    Одна из самых простых иллюстраций подхода - алгоритм вычисления функции Фибоначчи F(n) = F(n - 1) + F(n - 2). На рисунке 1 - его дерево рекурсии для F(6).

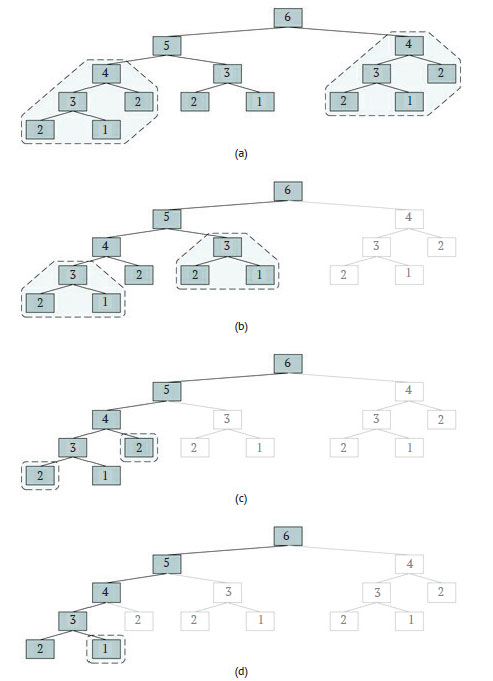
Рис.1. Перекрывающиеся подзадачи при вычислении чисел Фибоначчи по формуле F(n) = F(n - 1) + F(n - 2)

    На рисунке 1(a) мы имеем два одинаковых поддерева fibonacci(4) (корневой узел соответствует n = 4), то есть две перекрывающиеся подзадачи, которые выполняют одно и то же вычисление и возвращают один и тот же результат. Таким образом, по завершении первого вызова fibonacci(4) алгоритм может сохранить его результат в поисковой таблице и воспользоваться им впоследствии, чтобы не вызывать метод снова и не выполнять лишних вычислений. Эта стратегия позволяет нам исключить все вызовы, связанные с правым поддеревом дерева рекурсии, как показано на рисунке 1(b). Более того, усечение дерева рекурсии можно продолжить, если обратить внимание и на другие перекрывающиеся подзадачи. Как видно по рисунку 1(b), в оставшемся дереве есть ещё два одинаковых поддерева для n = 3 (отметим, что всего таких поддеревьев было три). Поэтому можно сохранить результат самого первого вычисления fibonacci(3) и при необходимости использовать его значение.

    Применение такого подхода ко всему исходному дереву рекурсии приводит к алгоритму с рекурсивным деревом (рисунок 1(d)), содержащим всего n узлов. Таким образом, за счет увеличения объёма памяти для хранения n промежуточных результатов F(i), где i = 1, ..., n, новому алгоритму требуется для выполнения линейное время. Увеличение скорости просто поражает, если вспомнить, что первоначальный алгоритм выполнялся за показательное время.

    В примере 10.5 приведён один из способов реализации нового подхода для функции Фибоначчи.

def fib_memoization(n, a):
    if n == 1 or n == 2:
        return 1
    elif a[n] > 0:
        return a[n]
    else:
        a[n] = fib_memoization(n - 1, a) \
               + fib_memoization(n - 2, a)  
        return a[n]


n = 100
print(fib_memoization(n, [0] * (n + 1)))

    Помимо параметра n, метод получает заполненный нулями список (таблицу) поиска а. Его длина - n + 1, так как индексы в языке Python начинаются с 0. Метод начинается с проверки начального условия. Поскольку оно всегда возвращает только константу 1, проще проверить начальное условие и вернуть его значение, чем искать его в списке. Таким образом, эта версия алгоритма не сохраняет значения начальных условий в списке поиска. В случае рекурсивного условия, если a_n > 0, значение F(n) уже сохранено в a_n (то есть a_n = F(n)). Если результат проверки рекурсивного условия - True, метод просто возвращает a_n, не выполняя рекурсивного вызова. В противном случае алгоритм работает, как функция fibonacci(), но прежде чем вернуть результат, он сохраняет его в a_n. В итоге метод позволяет вычислить числа Фибоначчи за линейное время, но требует дополнительного списка размера n. Однако это не влияет на пространственную сложность вычислений, поскольку функция fibonacci() тоже требует порядка n блоков памяти в программном стеке.

    На 116 шаге описаны два рекурсивных алгоритма решения задачи о самой длинной подстроке-палиндроме, время выполнения которой - показательная функция от длины исходной строки. Рассмотрим теперь основанное на мемоизации решение, выполняющееся за квадратичное время. В примере 10.6 приведена версия примера 7.7, но с мемоизацией.

def lps_memoization(s, L, i, j):
    if len(L[i][j]) > 0:
        return L[i][j]
    elif i > j:
        return ''
    elif i == j:
        L[i][j] = s[i]
        return s[i]
    else:
        if len(L[i + 1][j - 1]) > 0:   
            s_aux_1 = L[i + 1][j - 1]
        else:
            s_aux_1 = lps_memoization(s, L, i + 1, j - 1)  
            L[i + 1][j - 1] = s_aux_1

        if len(s_aux_1) == j - i - 1 and s[i] == s[j]:
            L[i][j] = s[i:j + 1]
            return s[i:j + 1]
        else:
            if len(L[i + 1][j]) > 0:
                s_aux_2 = L[i + 1][j]
            else:
                s_aux_2 = lps_memoization(s, L, i + 1, j)
                L[i + 1][j] = s_aux_2

            if len(L[i][j - 1]) > 0:
                s_aux_3 = L[i][j - 1]
            else:
                s_aux_3 = lps_memoization(s, L, i, j - 1)
                L[i][j - 1] = s_aux_3

            if len(s_aux_2) > len(s_aux_3):
                return s_aux_2
            else:
                return s_aux_3

s = 'bcaac'
L = [['' for i in range(len(s))] for j in range(len(s))]
print(lps_memoization(s, L, 0, len(s) - 1))

    Помимо начальной строки s длины n, метод имеет три дополнительных параметра. Во-первых, он использует нижний (i) и верхний (j) индексы, задающие подстроку поиска самой длинной подстроки-палиндрома. Кроме того, он использует матрицу L размерности n * n для хранения самых длинных подстрок-палиндромов, найденных методом (конечно, можно реализовать более эффективную версию, которая вместо матрицы сохраняет в любой момент времени только самую длинную подстроку-палиндром, найденную методом). В частности, элемент L_i,j, будет самой длинной подстрокой-палиндромом, найденной в подстроке s_i...j, где i ≤ j. Первоначально метод вызывается со строкой s, матрицей L с пустыми элементами, а также верхним и нижним индексами 0 и n - 1 соответственно.

    Сначала метод проверяет, решалась ли ранее такая задача. В этом случае элемент L, будет содержать непустую строку, которую метод может сразу возвратить (строки 2 и 3). Затем проверяется условие i > j, возвращающее в случае True пустую строку. В строках 6-8 алгоритм проверяет, состоит ли заданная своими индексами подстрока из единственного символа. В этом случае он сохраняется в таблице L и возвращается в качестве результата. Остальная часть кода относится к рекурсивным условиям. В строках 10-14 метод ищет самую длинную подстроку-палиндром в s_i+1...j-1, но вызывает рекурсивный метод, только если решение еще не было вычислено и сохранено в L. Затем, если подстрока s_i+1...j-1 - является палиндромом (len(s_aux_1) == j - i - 1), метод проверяет условие s_i = s_j (строка 16). Если оно выполняется, то s_i...j будет самым длинным палиндромом, и метод сохранит и вернёт его (строки 17 и 18). Если же s_i...j не является палиндромом, метод выполнит два рекурсивных вызова, аналогичных вызовам в строках 10 и 11 из примера 7.7, и сохранит их результаты, но только если соответствующие подзадачи не были решены ранее (строки 20-30). В заключение метод возвращает самую длинную из двух строк-палиндромов, соответствующих этим двум подзадачам.

    Алгоритм имеет квадратичную сложность вычисления, так как, по сути дела, создаёт двумерную матрицу L и решает подзадачу не более одного раза. Поэтому он гораздо эффективнее метода из примера 7.7, требующего экспоненциального времени.

    На следующем шаге мы рассмотрим граф зависимости и динамическое программирование.

Предыдущий шаг Содержание Следующий шаг