На этом шаге мы рассмотрим эти понятия.
Перебор с возвратами - это общая стратегия решения вычислительных задач, состоящая в выборе одного из конечного дискретного множества вариантов (элементов). Таким образом, формально говоря, перебор с возвратами - это стратегия поиска решения в "дискретном (конечном) пространстве состояний". Кроме того, это - метод решения "в лоб" в том смысле, что поиск является исчерпывающим. Другими словами, если решение существует, то алгоритм перебора с возвратами обязательно его найдёт.
Метод ведёт поиск решения с созданием и обновлением частичного решения (partial solution), которое в итоге может стать правильным полным решением (complete solution) задачи. Частичные решения создаются путём пошагового наращивания количества элементов-кандидатов (candidate) в последовательных рекурсивных вызовах. Таким образом, неявно подразумевается некий порядок следования кандидатов в решении. В этом смысле частичное решение можно считать "префиксом" полного решения. Если полное решение задачи - список, то частичное решение - это просто его подсписок из нескольких первых элементов (светлая область на рисунке 1(a)).
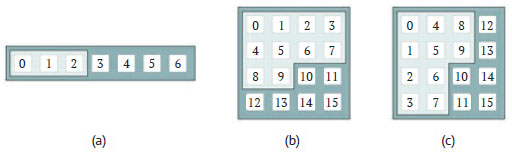
Рис.1. Частичные решения внутри полных решений для списка или матрицы
Если же полное решение представляет собой двумерную матрицу, то её элементы необходимо линейно упорядочить каким-то образом. Два самых естественных способа - упорядочить элементы матрицы по строкам или по столбцам, как показано на рисунках 1(b) и 1(c) соответственно. В этом случае частичное решение будет представлять собой множество из нескольких первых элементов матрицы, согласно выбранному линейному порядку.
Ключевой момент перебора с возвратами - эффективная проверка частичного решения на соответствие заданным ограничениям задачи. Если она успешна, то появляется возможность довести частичное решение до полного правильного решения. Если же правильное частичное решение после добавления к нему нового элемента оказывается недопустимым, алгоритм должен вернуться ("откатиться") к другому, предыдущему, правильному частичному решению и продолжить перебор других, ещё не рассмотренных вариантов. Таким образом, алгоритмы перебора с возвратами выполняют исчерпывающий перебор вариантов, но для некоторых задач могут оказаться довольно эффективными за счёт сокращения тех частичных решений, которые определённо не могут привести к правильным полным решениям.
Первый вопрос при решении задач методом перебора с возвратами - выбор конкретной формы или структуры данных для решений. Как правило, они реализуются в виде списка или матрицы. В частности, для задачи размещения n ферзей первое, что приходит в голову, - это представить решения задачи в виде логической матрицы n*n, в которой n истинных значений соответствуют тем клеткам шахматной доски, где расположены ферзи. Частичные решения будут иметь ту же структуру, но включать меньше, чем n ферзей (разместив n-го ферзя, мы получим либо неправильное, либо полное решение задачи). Однако, несмотря на естественность и простоту матричного представления, такой выбор структуры данных нельзя признать удачным, поскольку он приводит к неэффективному алгоритму. Так как методы перебора с возвратами выполняют исчерпывающий перебор, алгоритму для размещения очередного ферзя в одной из клеток шахматной доски придётся просматривать всю матрицу по строкам или столбцам. Это займёт слишком много времени, ведь размещать ферзя, скажем, в столбце, где уже стоит ферзь, алгоритму нет необходимости. Вместо этого алгоритм должен просто перейти к следующему столбцу.
Поэтому более подходящая структура данных для представления решений этой задачи - простой список длины n. В этом случае индексы списка могут представлять номера вертикалей шахматной доски, а значения элементов списка - номера горизонталей, где стоят ферзи. Другими словами, если x - список, представляющий решение, и ферзь стоит в столбце (вертикали) i и строке (горизонтали) j, то xi = j. Например, если столбцы пронумерованы слева направо, а строки - сверху вниз, начиная с нуля, то решение на рисунке 1 185 шага соответствует списку [1, 3, 0, 2]. Использующий такой список алгоритм, (правильно) разместив ферзя в строке для определённого столбца (i), может попытаться разместить ферзя в следующем столбце (i + 1). Кроме того, он может отслеживать строки, где уже стоит ферзь, чтобы не размещать в них следующих ферзей.
На следующем шаге мы рассмотрим рекурсивную структуру таких алгоритмов.
