На этом шаге мы рассмотрим работу такой структуры.
Чтобы понять принцип работы алгоритма перебора с возвратами, рассмотрим его дерево рекурсии. На рисунке 1 приведено дерево рекурсии для метода перебора с возвратами, который находит одно решение задачи четырёх ферзей.
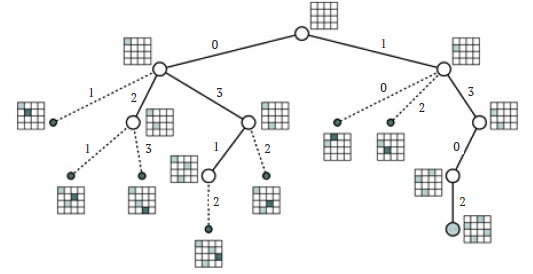
Рис.1. Дерево рекурсии алгоритма перебора с возвратами, который находит одно из решений задачи четырёх ферзей
Корневой узел дерева представляет собой первый вызов метода, где частичное решение в виде квадратной доски размером 4*4 (но представленное списком) пусто. Все последующие вызовы метода выполняются в порядке прямого (preorder) обхода дерева рекурсии. Первый рекурсивный вызов, связанный с левым потомком корня, размещает ферзя (затенённая клетка доски) в первой строке первого столбца. Метка "0" над ветвью дерева обозначает номер строки, на которую поставлен ферзь. Поскольку это частичное решение удовлетворяет ограничениям задачи, метод может продолжить размещение ферзей во втором столбце. В частности, он начинается с исключения попытки размещения ферзя в первой строке, поскольку он там уже есть. Затем алгоритм проверяет, можно ли разместить ферзя во второй строке. Очевидно, что этого сделать нельзя, потому что два ферзя оказались бы на одной диагонали. Значит, такое частичное решение неверно, и алгоритм не должен рассматривать его дальше. Другими словами, он не выполняет последующих рекурсивных вызовов с таким (недопустимым) частичным решением. Такие ветви обозначены на рисунке пунктиром.
Дальше метод ставит ферзя в третью строку, что приводит к правильному частичному решению. Следовательно, алгоритм может попытаться разместить ферзя в третьем столбце. Очередная свободная строка - вторая, но эта попытка приводит к недопустимому частичному решению. Размещение ферзя в четвёртой строке также нарушает условия задачи. Поскольку других вариантов нет, алгоритм "откатывается" к узлу с одним ферзём в первом столбце первой строки. Затем метод рассматривает все возможные частичные решения, которые возникают после размещения ферзя в 4-й строке 2-го столбца. Поскольку и в этом случае ни одного правильного решения нет, алгоритм вынужден будет вернуться к начальному узлу. Отметим, что на данном этапе метод выполняет полный перебор решений, когда ферзь стоит в первой строке первого столбца. На следующем этапе алгоритм продолжает перебор вариантов, начав с размещения ферзя на второй строке первого столбца. Та же самая процедура повторяется до тех пор, пока в конце концов метод не сможет разместить четырёх ферзей, которые не угрожают друг другу. В этом случае он может либо прекратить поиск, если требовалось найти только одно решение, либо продолжить его, чтобы найти все решения.
Дерево рекурсии демонстрирует также несколько особенностей алгоритма. Во-первых, узлы соответствуют рекурсивным вызовам метода, для которых частичное решение (входной параметр метода) правильно. Маленькие темные узлы, "висящие" на пунктирных ветвях, обозначают возможные вызовы метода в тех случаях, когда соответствующие им частичные решения оказываются правильными. Кроме того, обратите внимание, что для каждого такого неосуществлённого рекурсивного вызова указан новый элемент, добавляемый к частичному решению. Другими словами, частичные решения из к элементов связаны с узлами глубины k. Следовательно, полные решения достигаются в листовых узлах глубины n. Таким образом, путь от корня до узла определяет частичное решение или, если узлом является лист, полное решение. Например, найденное алгоритмом решение [1, 3, 0, 2] - это список меток тех ветвей, по которым пролегает путь от корня до листа-решения. Кроме того, поскольку значения в списке всегда представляют только различные строки, решение задачи четырёх ферзей - это фактически одна из перестановок номеров строк, то есть первых n неотрицательных целых чисел. Поэтому полное дерево перебора всех вариантов имело бы n! листьев, а это довольно большая величина даже для малых значений n. Однако на рисунке 1 видно, что дерево рекурсии можно существенно сократить за счёт исключения из рассмотрения недопустимых частичных решений, что является ключевым моментом в построении эффективных алгоритмов перебора.
Подобные моменты будут выявляться и в других задачах и примерах последующих шагов. В частности, в задаче о размещении n ферзей, которая вместе с кодом алгоритма её решения подробно разбирается далее. На практике сокращение деревьев рекурсии ради повышения эффективности алгоритмов перебора с возвратами достигается за счёт отбрасывания недопустимых решений.
На следующем шаге мы рассмотрим генерацию комбинаторных объектов.
