На этом шаге мы рассмотрим пример использования таких решений.

    На рисунке 1 приведено двоичное дерево рекурсии алгоритма, генерирующего восемь подмножеств, которые можно создать на множестве из трёх различных элементов.

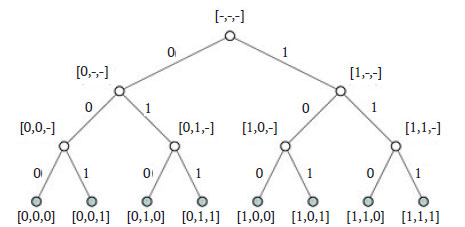
Рис.1. Дерево рекурсии алгоритма генерации всех подмножеств множества из трёх элементов

    Каждое подмножество задаётся двоичным списком из n нулей или единиц (конечно, допускаются и логические значения). Например, для исходного списка элементов [a, b, с] список [1, 0, 1] будет обозначать подмножество {a, с}. Этот двоичный список - частичное решение, которое становится полным по достижении методом листа дерева рекурсии, а сами двоичные цифры - это элементы-кандидаты в процессе его формирования. При выполнении рекурсивного вызова метод просто добавляет нового кандидата (двоичная цифра над ветвью дерева) к частичному решению (указано рядом с узлом дерева), передаваемому методу в качестве аргумента. Исходная длина списка - n, но его элементы не определены. По достижении начального условия метод генерирует одно из 2n возможных подмножеств в одном из листьев дерева рекурсии. В этом случае список содержит n уже определённых элементов и представляет собой полное решение.

    В примере 12.1 приведён алгоритм, соответствующий дереву рекурсии на рисунке 1 и печатающий каждое подмножество с помощью метода print_subset_binary().

def generate_subsets(i, sol, elements):
    # Базовый вариант
    if i == len(elements):
        # Печать полного решения
        print_subset_binary(sol, elements)
    else:
        # Генерация элементов-кандидатов
        for k in range(0, 2):

            # Включить кандидата в частное решение
            sol[i] = k

            # Генерация элемента в позиции i+1
            generate_subsets(i + 1, sol, elements)

            # Удалить кандидата из частного решения
            sol[i] = None  # по желанию


def generate_subsets_wrapper(elements):
    sol = [None] * (len(elements))
    generate_subsets(0, sol, elements)


def print_subset_binary(sol, elements):
    no_elements = True
    print('{', end='')
    for i in range(0, len(sol)):
        if sol[i] == 1:
            if no_elements:
                print(elements[i], sep='', end='')
                no_elements = False
            else:
                print(', ', elements[i], sep='', end='')  
    print('}')

    Кроме исходного множества (списка) из n элементов, процедура метода получает также список sol (частичное решение) из n элементов со значениями None, присвоенными ему в методе-оболочке generate_subsets_wrapper(). Обратите внимание, что на каждом уровне метод, спускаясь вниз по дереву рекурсии, включает в частичное решение нового кандидата. По этой причине он использует третий параметр i - индекс элемента списка (частичного решения), куда будет помещена новая цифра 0 или 1. Кроме того, i также соответствует уровню узла рекурсивного вызова, отвечающего за добавление нового элемента в частичное решение. Поскольку рекурсивный метод перебора с возвратами generate_subsets() добавляет новую цифру 0 или 1, начиная с индекса 0 списка частичного решения, в generate_subsets_wrapper() индексу i присваивается начальное значение 0.

    Метод generate_subsets() в строке 3 проверяет, является ли частичное решение sol полным, то есть совпадает ли значение i с n. Эта проверка отвечает начальному условию, когда метод должен просто напечатать решение (строка 5). В рекурсивном условии процедура должна дважды выполнить рекурсивный вызов, чтобы включить новых кандидатов в частичное решение. Это достигается простым циклом, в котором переменная k принимает значения 0 или 1 (строка 8), а элемент частичного решения sol[i] получает значение k (строка 11). Все алгоритмы перебора с возвратами, приведенные далее, также будут использовать цикл для перебора всех возможных кандидатов, которых можно добавить к частичному решению. После этого процедура вызывает саму себя (строка 14) с изменённым частичным решением и увеличенным на 1 индексом i, чтобы добавить нового кандидата (если частичное решение ещё не стало полным).

    Строка 17 не обязательна, поскольку метод и без неё работает правильно. Она включена в процедуру на тот случай, если такое действие понадобится в других алгоритмах перебора с возвратами. Обратите внимание, что когда определённый рекурсивный вызов в узле дерева завершается, управление передаётся его родителю, для которого позиция i частичного решения уже не имеет значения, и строка 17 явно отражает этот факт. Однако метод работает и без неё, потому что по достижении начального условия (когда частичное решение становится полным) он всего лишь печатает подмножество, а присваивание в строке 11 просто обнуляет этот элемент при k = 1. Чтобы проследить изменения частичного решения, рекомендуется выполнить программу шаг за шагом с помощью отладчика (со строкой 17 или без неё).

    Например, вызов generate_subsets_wrapper(['a','b','c']) даёт следующий результат:

{}
{c}
{b}
{b, c}
{a}
{a, c}
{a, b}
{a, b, c} 

    На следующем шаге мы рассмотрим частичные решения переменной длины.

Предыдущий шаг Содержание Следующий шаг