На этом шаге мы рассмотрим пример использования таких решений.

В предыдущем алгоритме частичные решения имели фиксированную длину n. Такая процедура может работать со списками или массивами, размер которых не меняется. В этом случае для указания индекса добавляемого к частичному решению элемента был необходим параметр i. Если же вместо частичных решений фиксированной длины использовать частичные решения переменного размера, то необходимость в параметре i отпадает. На рисунке 1 приведено другое рекурсивное дерево с той же, как на рисунке 1 предыдущего шага, структурой, однако метки (частичные решения) рядом с узлами (вызовами рекурсивного метода) теперь не содержат неопределённостей.

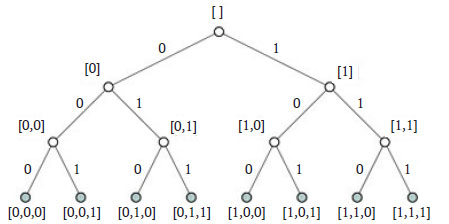
Рис.1. Двоичное дерево рекурсии альтернативного алгоритма генерации всех подмножеств множества из трёх элементов

В примере 12.2 приведён соответствующий этому подходу метод, который очень похож на код примера 12.1.

Пример 12.2. Альтернативная печать всех подмножеств множества, заданного списком

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

def generate_subsets_alt(sol, a):
    # Base case
    if len(sol) == len(a):
        # Печать полного решения
        print_subset_binary(sol, a)
    else:
        # Генерация элементов-кандидатов
        for k in range(0, 2):

            # Включить кандидата в частное решение
            sol = sol + [k]

            # Генерация элемента в позиции i+1
            generate_subsets_alt(sol, a)

            # Удалить кандидата из частного решения
            del sol[-1]


def print_subset_binary(sol, elements):
    no_elements = True
    print('{', end='')
    for i in range(0, len(sol)):
        if sol[i] == 1:
            if no_elements:
                print(elements[i], sep='', end='')
                no_elements = False
            else:
                print(', ', elements[i], sep='', end='')  
    print('}')


def generate_subsets_alt_wrapper(elements):
    sol = []
    generate_subsets_alt(sol, elements)

Архив с файлом можно взять здесь.

В начальном условии он просто печатает решение, если оно содержит n элементов. В рекурсивном условии он использует тот же цикл, в котором в конец частичного решения он добавляет 0 или 1, а затем вызывает сам себя. В этом случае код в строке 17 становится необходимым, так как метод должен "отменить" все изменения в частичном решении до рекурсивного вызова самого себя. Если в примере 12.1 алгоритм обнуляет единицу в частичном решении, то в данном случае метод должен сначала удалить 0 из списка, чтобы затем правильно добавить в него 1. Таким образом, вызов рекурсивного метода подразумевает добавление нового элемента к частичному решению (строка 14) и поэтому должен удалить старый элемент (строка 17) по возвращении из рекурсивного вызова. Строка 17 из примера 12.1 имеет тот же смысл, но в ней нет необходимости. Что касается эффективности, то динамическое добавление элементов в структуру данных и их удаление из неё может занимать значительное время. Таким образом, зачастую лучше выделить для частичного решения фиксированный объём памяти и обновлять его, не меняя его размера. В этом отношении код в примере 12.1 выполняется быстрее, чем метод generate_subsets_alt(). Наконец, для этого альтернативного алгоритма метод-оболочка должен инициализировать частичное решение пустым списком.

Со следующего шага мы начнем рассматривать перестановки.

Предыдущий шаг Содержание Следующий шаг