На этом шаге мы рассмотрим пример, реализующий такой подход.

    В примере 12.3 приводится первый метод, соответствующий дереву рекурсии на рисунке 1 предыдущего шага.

def generate_permutations(i, sol, elements):
    # Базовый вариант
    if i == len(elements):
        print_permutations(sol)  # комплексное решение
    else:
        # Генерация элементов-кандидатов
        for k in range(0, len(elements)):

            # Проверка валидности кандидатов
            if not elements[k] in sol[0:i]:

                # Включить кандидата в частное решение
                sol[i] = elements[k]

                # Генерация элемента в позиции i+1
                generate_permutations(i + 1, sol, elements)  

                # Удалить кандидата из частного решения
                sol[i] = None  # по желанию


def generate_permutations_wrapper(elements):
    sol = [None] * (len(elements))
    generate_permutations(0, sol, elements)


def print_permutations(sol):
    for i in range(0, len(sol)):
        print(sol[i], ' ', end='')
    print()

    Поскольку i - это число элементов в частичном решении sol, первый условный оператор if выполняет проверку начального условия. Если результат - True, процедура просто печатает перестановку, сохранённую в sol. Иначе алгоритм в цикле начинает добавлять в частичное решение новых кандидатов из исходного списка. Для каждого значения от 0 до n - 1 счётчика цикла k в роли индекса элемента списка алгоритм выполняет проверку на отсутствие кандидата в частичном решении (строка 10). Стоит отметить, что, несмотря на лаконичность записи условия в строке 10, оно может потребовать в самом худшем случае i проверок значений кандидатов. Если кандидата ещё нет в частичном решении, метод добавляет его (строка 13) и выполняет рекурсивный вызов с увеличением i на единицу (строка 16). Следующая за рекурсивным вызовом строка 19 с "отклонением" кандидата не обязательна, так как метод всё равно перезаписывает значение sol[i]. Иными словами, нет нужды присваивать sol[i] значение None. Тем не менее эта строка включена в код, чтобы он точно соответствовал дереву рекурсии на рисунке 1 192 шага.

    Метод generate_permutations_wrapper() - это процедура-оболочка, необходимая для инициализации частичного решения n значениями None и вызова рекурсивного метода generate_permutations() с нулевым значением i. В заключение код содержит процедуру печати через пробел элементов списка (перестановки) sol.

    Итак, подобно остальным алгоритмам этого раздела, метод использует цикл для подбора возможных кандидатов на включение в частичное решение. Без учёта проверок ограничений во внутренних узлах дерева данный алгоритм может привести к полному n-арному дереву рекурсии (у каждого внутреннего узла дерева n дочерних узлов) с nⁿ листьями. Конечно, можно проверять правильность частичных решений в каждом из этих nⁿ листьев. Но гораздо лучше проверять допустимость кандидата во внутреннем узле и отказываться от ненужных рекурсивных вызовов, если алгоритм обнаруживает совершенно недопустимое частичное решение. Условие в строке 6 обеспечивает такую проверку и резко ускоряет алгоритм, сокращая дерево рекурсии, как показано на рисунке 1.

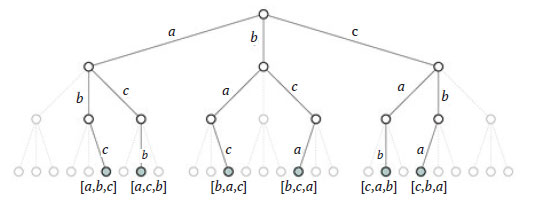
Рис.1. Сокращение дерева рекурсии за счёт исключения недопустимых частичных решений

    Более светлые узлы и ветви дерева - это те вызовы метода полного троичного дерева, которые не выполняются (сокращаются) благодаря условию в строке 6. Получающееся дерево рекурсии (изображенное более тёмными узлами и ветвями) становится идентичным изображённому на рисунке 1 192 шага и содержит n! листьев. Хотя эта величина тоже внушительна даже для относительно малых значений n, она всё же значительно меньше nⁿ.

    На следующем шаге мы рассмотрим проверку правильности частичных решений с использованием дополнительных структур данных.

Предыдущий шаг Содержание Следующий шаг