На этом шаге мы дадим краткую характеристику рассмотренных далее алгоритмов.
Начиная с этого шага, рассматриваются два схожих алгоритма, которые печатают все возможные перестановки n различных элементов заданного списка (множества). В первом частичное решение (перестановка) представлено списком индексов от 0 до n - 1, указывающих на позиции элементов в исходном списке. Например, для исходного списка [a, b, с] частичное решение [1, 2, 0] означает перестановку [b, с, а]. Во всех последующих алгоритмах частичное решение (перестановка) будет состоять просто из элементов исходного списка (и пустых значений None). На рисунке 1 показана структура дерева рекурсии для такого алгоритма на примере списка [a, b, с].
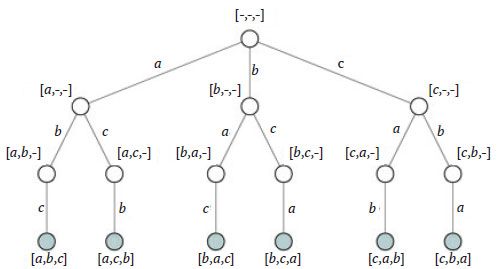
Рис.1. Дерево рекурсии алгоритма генерации всех перестановок множества из трёх элементов
Заметьте, что список с частичным решением имеет длину n, но только первые его элементы значимы. При первом вызове метода частичное решение пусто, то есть все его элементы установлены в None. Кроме того, процедуры получают (первоначально установленный в ноль) параметр i, который задаёт количество уже включённых в частичное решение элементов-кандидатов. Таким образом, он указывает место нового кандидата в частичном решении и уровень узла в дереве рекурсии или глубину рекурсивного вызова.
Метод начинается с добавления одного из n элементов-кандидатов исходного списка в первую позицию частичного решения. Поскольку вариантов всего n, корневой узел имеет n дочерних узлов. На следующем уровне дерева методы вызывают себя (n - 1) раз, так как элемент, помещённый в первую позицию, уже не может снова появиться в перестановке. Точно так же на следующем уровне частичные решения содержат по два элемента, а методы вызывают себя (n - 2) раза. И так повторяется до тех пор, пока метод не достигает начального условия в листе дерева рекурсии, где частичные решения становятся полными перестановками.
В следующих шагах описываются способы проверки правильности частичного решения в каждом из двух методов, в чём и заключается их основное различие.
На следующем шаге мы рассмотрим проверку правильности частичных решений без использования дополнительных структур данных.
