На этом шаге мы рассмотрим особенности решения этой задачи.

    Головоломка судоку - из разряда так называемых задач удовлетворения ограничений. Её цель состоит в том, чтобы заполнить сетку 9х9 цифрами от 1 до 9 (или любыми другими девятью различными символами, так как их числовые значения не важны). Каждая из цифр может появиться только однажды в каждой строке, каждом столбце и каждой из девяти неперекрывающихся подсеток размером 3х3, называемых также блоками, которые покрывают сетку 9х9. На рисунке 1 показан экземпляр задачи с частично заполненной исходными цифрами сеткой.

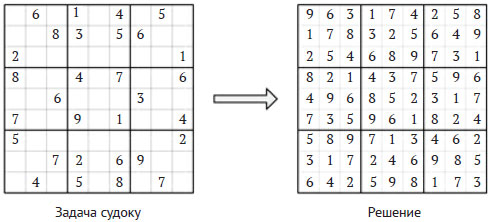
Рис.1. Задача судоку и ее решение

    Правильно поставленная задача должна иметь только одно решение (начальная сетка должна содержать не меньше 17 цифр).

    Для представления сетки судоку мы будем использовать список списков цифр, где цифра 0 будет обозначать пустую клетку. Частичные решения будут частично заполненными сетками, а алгоритм должен неким образом пронумеровать все клетки сетки, чтобы можно было расширять частичные решения новыми цифрами. Приводимый ниже алгоритм будет расширять частичные решения в порядке следования строк, начав добавлять цифры-кандидаты с верхнего ряда сетки слева направо и так далее для каждой последующей строки. Таким образом, алгоритм найдёт решение, если сумеет поместить правильную цифру в последнюю клетку последней строки.

    В рекурсивном условии метод генерирует девять возможных кандидатов для заполнения пустой клетки. Таким образом, каждый узел дерева рекурсии мог бы иметь до девяти дочерних узлов, как показано на рисунке 2(a).

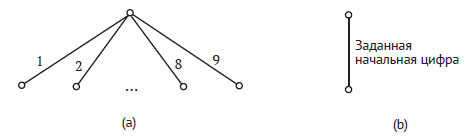
Рис.2. Рекурсивные условия при решении судоку

    Однако у этой задачи есть особенность, которая не встречалась ни в одной из предыдущих задач: присутствие в частичном решении (сетке) заранее заданных фиксированных элементов (клеток с цифрой). Это значит, что при обработке клетки с цифрой алгоритм должен просто пропустить её (без расширения частичного решения) и выполнить рекурсивный вызов, обрабатывающий следующую клетку. Это требует включения второго рекурсивного условия, которое приведено на рисунке 2(b).

    В примерах 12.10 и 12.11 приводится решающая задачу процедура перебора с возвратами и несколько вспомогательных функций.

def solve_sudoku_all_sols(row, col, S):
    # Проверьте, завершено ли судоку
    if row == 9:
        print_sudoku(S)  # распечатать готовое судоку
        print()
    else:
        # Проверьте, является ли цифра S[row][col] начальным фиксированным символом  
        if S[row][col] != 0:

            # Перейти к новой ячейке в порядке возрастания строк
            (new_row, new_col) = advance(row, col)

            # Попробуйте расширить частичное решение
            solve_sudoku_all_sols(new_row, new_col, S)
        else:
            # Сгенерировать цифры-кандидаты
            for k in range(1, 10):

                # Проверить, является ли цифра k допустимым кандидатом
                if is_valid_candidate(row, col, k, S):

                    # Включить цифру в ячейку (row, col)
                    S[row][col] = k

                    # Перейти к новой ячейке в порядке возрастания строк
                    (new_row, new_col) = advance(row, col)

                    # Попытка расширить частичное решение
                    solve_sudoku_all_sols(new_row, new_col, S)

            # Очистить ячейку (row, col)
            S[row][col] = 0


# Вычислить следующую ячейку в порядке возрастания по строкам
def advance(row, col):
    if col == 8:
        return (row + 1, 0)
    else:
        return (row, col + 1)

    Рекурсивная функция solve_sudoku_all_solutions() допускает в том числе и неправильную постановку задачи, когда она может иметь несколько решений или даже ни одного. Таким образом, процедура выдаёт все правильные решения задачи для заданной сетки судоку.

    Например, если верхний ряд судоку на рисунке 1 заменить пустой строкой, то существует 10 различных способов заполнения цифрами сетки судоку.

    Параметры рекурсивной процедуры - пара координат (row и col) клетки, куда она пытается внести цифру для расширения частичного решения, а также само частичное решение S, представленное списком списков цифр. Так как процедура расширяет частичное решение построчно, начиная с клетки (0, 0), правильное решение достигается при row = 9. При выполнении начального условия она просто выводит сетку судоку (строка 4). В противном случае метод проверяет, не заполнена ли текущая клетка, то есть не содержит ли она одну из заранее заданных фиксированных цифр. Если да, то такая клетка пропускается и процедура вызывает себя (строка 14) с координатами (вычисленными в строке 11) следующей по порядку клетки.

    Во втором рекурсивном условии функция использует цикл для генерации девяти возможных кандидатов на включение в пустую клетку. Затем в строке 20 она проверяет, можно ли включить кандидата k в клетку (row, col) частичного решения S. Если можно, то процедура включает кандидата в частичное решение (строка 23) и продолжает работу, выполняя рекурсивный вызов со следующей клеткой (строка 29). По завершении цикла функция должна отменить произведённые в клетке изменения, сделав её пустой (строка 32). Это необходимо для последующего анализа решений. Отметим, что клетка должна быть пустой, чтобы алгоритм мог снова обработать её после отката к одной из предыдущих клеток.

    Вспомогательные функции:

• а) функция, возвращающая пару координат следующей по порядку клетки (см. пример 12.10);
• b) функция, определяющая, нарушает ли размещённая в некоторой строке и столбце цифра ограничения задачи, где переменные box_row и box_col задают верхнюю левую клетку блока 3х3;
• с) функция, считывающая сетку судоку из текстового файла, каждая строка которого содержит девять строк цифр исходного судоку, разделённых символом пробела;
• d) метод для вывода сетки;
• e) код, считывающий и решающий судоку.

import math


# Проверить, является ли цифра в ячейке (row, col) допустимой
def is_valid_candidate(row, col, digit, S):
    # Проверить конфликт в столбце
    for k in range(0, 9):
        if k != col and digit == S[row][k]:
            return False

    # Проверить конфликт в стоке
    for k in range(0, 9):
        if k != row and digit == S[k][col]:
            return False

    # Проверить конфликт в блоке
    box_row = math.floor(row / 3)
    box_col = math.floor(col / 3)
    for k in range(0, 3):
        for n in range(0, 3):
            if (row != 3 * box_row + k
                    and col != 3 * box_col + n):
                if digit == S[3 * box_row + k][3 * box_col + n]:  
                    return False

    return True


# Распечатать сетку судоку в консоли
def print_sudoku(S):
    for s in S:
        print(*s)

# Прочитать сетку судоку из текстового файла
def read_sudoku(filename):
    file = open(filename, 'r')
    S = [[None] * 9] * 9
    i = 0
    for line in file.readlines():
        S[i] = [int(x) for x in line.split(' ')]
        i = i + 1
    file.close()
    return S


S = read_sudoku('sudoku01_input.txt')  # Исходный файл
solve_sudoku_all_sols(0, 0, S)

    Со следующего шага мы начнем разбирать задачу о рюкзаке.

Предыдущий шаг Содержание Следующий шаг