На этом шаге мы рассмотрим решение этой задачи.

    На этом шаге описывается алгоритм перебора с возвратами для поиска пути в лабиринте (рисунок 1(a)), который представляет собой прямоугольный массив клеток - пустых и непустых.

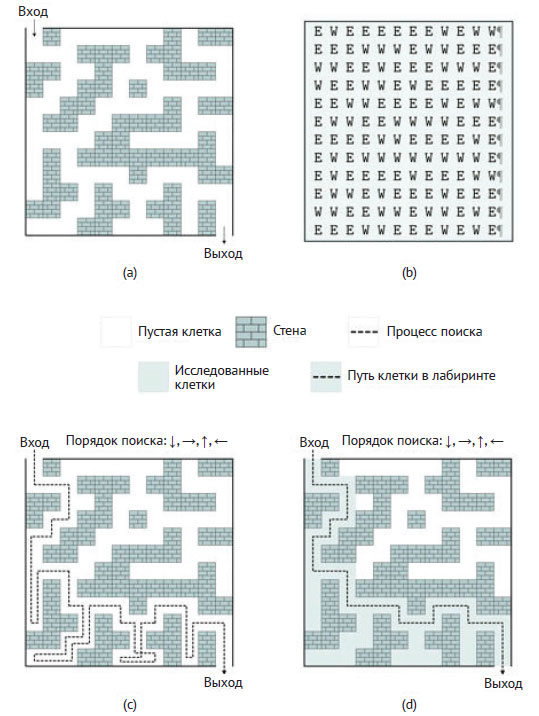
Рис.1. Задача поиска пути в лабиринте и её решение перебором с возвратами при определённом порядке поиска

    Пустые клетки - это проходы по лабиринту, непустые - это его стены или перегородки. Мы же представим его в виде списка списков M (состоящего из символов), где первый список в списке - это верхний ряд (слева направо) клеток лабиринта, второй список - следующий под ним ряд и т. д. Чтобы задать лабиринт, пользователю нужно записать каждый ряд клеток в виде строки разделённых пробелом символов (см. рисунок 1(b)), где 'E' обозначает пустую клетку, по которой можно пройти, a 'W' - стену. Поскольку большие лабиринты вводить вручную трудно, можно хранить массив символов в файле, который можно загрузить автоматически при выполнении программы (что также удобно для отладки). Кроме самого лабиринта, методу нужны параметры, задающие клетки входа в лабиринт и выхода из него. На рисунке это верхняя левая и нижняя правая клетки соответственно. Таким образом, в данном примере начальная клетка - это М[0][0].

    Алгоритм перебора с возвратами выполняет полный перебор путей, начинающихся в начальной клетке и заканчивающихся в конечной клетке. Достигнув на каком-то промежуточном шаге некоторой клетки, алгоритм должен рассмотреть каждое из четырёх возможных направлений продолжения пути к соседней клетке - вверх, вниз, вправо или влево. Поскольку конечная клетка находится в нижнем правом углу лабиринта, алгоритм может начать поиск пути с попытки пойти сначала вниз, затем вправо, потом вверх и, наконец, влево. При таком порядке поиска пути метод выполнит шаги, показанные на рисунке 1(c). Отметим, что, достигнув пустой клетки, метод сначала пытается продолжить путь вниз. Если это невозможно, он пытается сделать шаг вправо, затем вверх и, наконец, влево. Если это невозможно ни в одном из этих четырёх направлений, он должен "откатиться" назад к предыдущей клетке и попытаться найти другой путь. В нашем примере начальная клетка находится в позиции (0, 0) и соответствует строке 0 и столбцу 0. Метод помечает эту клетку как часть текущего пути, присваивая M[0][0] значение 'P'. Первый шаг возможен только в клетку (1, 0), которая тоже помечается символом 'P'. Из неё метод пытается продвинуться вниз, но натыкается на стену в клетке (2, 0). Поскольку дальше пути нет, алгоритм делает попытку шагнуть вправо, которая возможна, так как клетка (1, 1) пуста. Достигнув в какой-то момент клетки (6, 0), метод продолжит поиск пути с попытки пойти вниз. Этот путь приведёт его к тупиковой клетке (9, 0): снизу и справа - стены, слева - граница лабиринта, за пределы которого выходить нельзя, а сверху - клетка, заведшая метод в этот тупик. Поскольку алгоритм не может продвинуться ни в одном из направлений, он "откатывается" к клетке (8, 0), где он еще не пытался двигаться вправо, вверх или влево. Однако эти варианты тоже оказываются недопустимыми. То же самое происходит и после "отката" к клетке (7, 0). И только после возврата к клетке (6, 0) и исчерпывающего анализа всех возможных путей вниз от неё появляется возможность исследовать новые пути, ведущие от неё вправо. Этот процесс повторяется до тех пор, пока алгоритм не найдёт конечную клетку выхода из лабиринта. Решение приведено на рисунке 1(d), где все исследованные в процессе поиска выхода клетки затенены.

    Алгоритм перебора с возвратами может либо прекратить поиск решений, когда найдено одно из них, либо продолжить поиск других возможных решений. Мы рассмотрим алгоритм, который останавливается, как только находит путь в лабиринте. В связи с этим нужно иметь в виду, что порядок рассмотрения возможных направлений движения может приводить к различным решениям, как показано на рисунке 2.

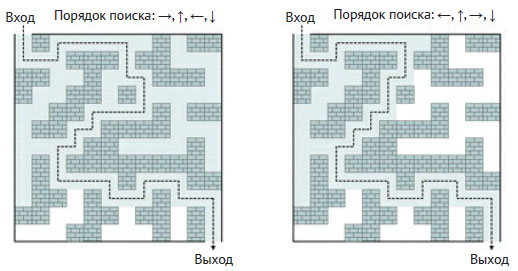
Рис.2. Различные пути в лабиринте в зависимости от порядка поиска

    Обратите внимание, что множества исследуемых в каждом случае клеток различны.

    Очевидно, что решение этой задачи не сводится к перестановкам клеток. Это видно хотя бы из того, что длина пути (то есть решение) непостоянна. Более того, хотя путь состоит из подмножества множества клеток лабиринта, эти подмножества являются упорядоченными. Значит, свести решение к генерации подмножеств множества тоже не удастся. По этим причинам мы представляем решение в виде символьной матрицы, в которой клетки определённого пути помечаются символом 'P'. Таким образом, частичное решение будет представлять собой исходный лабиринт, включающий путь от начальной клетки до некоторой пустой клетки, по достижении которой метод должен выбрать одну из четырёх клеток-кандидатов на включение её в частичное решение. Следовательно, мы приходим к рекурсивной декомпозиции задачи, показанной на рисунке 3, где r и c обозначают конкретные строку и столбец соответственно.

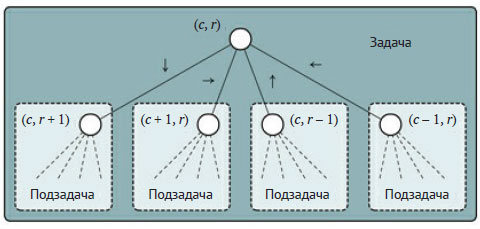
Рис.3. Декомпозиция задачи поиска пути в лабиринте

    Каждый узел дерева рекурсии будет иметь четыре дочерних узла, соответствующих четырём возможным направлениям движения. При этом алгоритм, прежде чем выполнить рекурсивный вызов с расширенным частичным решением, должен убедиться, что новая клетка пуста.

    В примере 12.8 приводится одна из реализаций алгоритма решения задачи методом перебора с возвратами.

def find_path_maze(M, row, col, incr, exit_row, exit_col):
    # Базовый случай: проверка, найден ли путь
    if row == exit_row and col == exit_col:
        return True  # Решение найдено
    else:
        sol_found = False
        # Генерация кандидатов
        k = 0
        while not sol_found and k < 4:

            # Новая ячейка-кандидат
            new_col = col + incr[k][0]
            new_row = row + incr[k][1]

            # Проверка кандидата на валидность
            if (new_row >= 0 and new_row < len(M)
                    and new_col >= 0 and new_col < len(M[0])
                    and M[new_row][new_col] == 'E'):

                # Добавить к пути (частичное решение)
                M[new_row][new_col] = 'P'

                # Пробуем расширить путь, начиная с новой ячейки
                sol_found = find_path_maze(
                    M, new_row, new_col, incr,
                    exit_row, exit_col)

                # Отметить как пустую, если новая ячейка не находится в решении  
                if not sol_found:
                    M[new_row][new_col] = 'E'

            k = k + 1

        return sol_found


def find_path_maze_wrapper(M, enter_row, enter_col,
                           exit_row, exit_col):
    # направления поиска
    incr = [(0, 1), (1, 0), (0, -1), (-1, 0)]

    M[enter_row][enter_col] = 'P'
    return find_path_maze(M, enter_row, enter_col, incr,
                          exit_row, exit_col)

    Параметры метода-оболочки - исходный лабиринт и четыре целых числа, которые задают координаты начальной (enter_row, enter_col) и конечной (exit_row, exit_col) клеток лабиринта. Кроме того, в нём объявляется список incr, определяющий направления движения при поиске пути, а также порядок выбора этих направлений. Каждая пара (x, у) в списке задаёт приращение номера столбца c и номера строки r клетки для перемещения из неё в новую соседнюю клетку с координатами (c + x, r + у). Порядок следования пар в списке определяет последовательность выбора направления поиска в этом алгоритме: вниз, вправо, вверх и влево. Заметьте, что добавление единицы к номеру строки означает движение вниз (поскольку первая строка расположена наверху лабиринта), тогда как добавление единицы к столбцу - движение вправо. В заключение метод-оболочка включает пустую начальную клетку в искомый путь в качестве первого шага к цели и возвращает (логическое) значение результата вызова рекурсивного метода перебора с возвратами.

    Первый параметр M рекурсивного метода find_path_maze() - это одновременно и исходный лабиринт, и частичное решение. Следующие два параметра - координаты последней клетки частичного пути в M, из которой алгоритм попытается расширить частичный путь перемещением в одну из соседних клеток последней клетки. Последние три параметра метода - это incr и координаты конечной клетки выхода из лабиринта.

    Рекурсивная функция find_path_maze() возвращает True, как только находит путь в лабиринте M. Она объявляет переменную sol_found с начальным значением False, которое меняется на True в начальном условии, когда алгоритм находит полное решение. В противном случае (случае рекурсивного условия) для генерации четырёх клеток-кандидатов она использует цикл while, который заканчивается, как только решение найдено. Переменные new_col и new_row определяют нового кандидата (строки 12 и 13), который сразу проверяется на правильность. В частности, он не должен выходить за пределы лабиринта (строки 16 и 17) и должен быть пустым (строка 18).

Если лабиринт по всему его периметру, за исключением входа и выхода, охватить стеной из непустых клеток, то строки 16 и 17 станут ненужными.

    Если клетка не нарушает ограничений задачи, метод присоединяет её к пути (строка 21) и в строках 24-26 вызывает сам себя, сохраняя результат вызова в sol_ found. Если решение не найдено, метод возвращает ей прежнее пустое значение 'E', исключая её таким образом из пути (строка 30). Это действие необходимо, так как в полном решении пометку 'P' могут иметь только клетки, образующие путь через лабиринт. Без этого действия все исследуемые клетки содержали бы символ 'P'. По завершении цикла метод просто возвращает значение sol_found (строка 34).

    Текст примера 12.9 служит необходимым дополнением к основному листингу 12.8. В нём приведён вспомогательный код, запускающий и выполняющий основной код, а также заполняющий и рисующий лабиринт.

import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from pr199_1 import find_path_maze_wrapper


def read_maze_from_file(filename):
    file = open(filename, 'r')
    M = []
    for line in file.readlines():
        M.append([x[0] for x in line.split(' ')])
    file.close()
    return M


gray = (0.75, 0.75, 0.75)
black = (0, 0, 0)
red = (0.75, 0, 0)
green = (0, 0.75, 0)


def draw_maze(M, enter_row, enter_col, exit_row, exit_col):
    nrows = len(M)
    ncols = len(M[0])
    fig = plt.figure()
    fig.patch.set_facecolor('white')
    ax = plt.gca()

    if enter_row is not None and enter_col is not None:
        ax.add_patch(Rectangle((enter_col, nrows - enter_row),
                               1, -1, linewidth=0, facecolor=green,
                               fill=True))
    if exit_row is not None and exit_col is not None:
        ax.add_patch(Rectangle((exit_col, nrows - exit_row),
                               1, -1, linewidth=0, facecolor=red,
                               fill=True))
    for row in range(0, nrows):
        for col in range(0, ncols):
            if M[row][col] == 'W':
                ax.add_patch(Rectangle((col, nrows - row), 1, -1,
                                       linewidth=0, facecolor=gray))
            elif M[row][col] == 'P':  
                circ = plt.Circle((col + 0.5, nrows - row - 0.5),
                                  radius=0.15, color=black, fill=True)  
                ax.add_patch(circ)
    ax.add_patch(Rectangle((0, 0), ncols, nrows, edgecolor=black,
                           fill=False))
    plt.axis('equal')
    plt.axis('off')
    plt.show()


M = read_maze_from_file('maze_01.txt')  # исходный файл
# Enter at top-left, exit bottom-right
if find_path_maze_wrapper(M, 0, 0, len(M) - 1, len(M[0]) - 1):
    draw_maze(M, 0, 0, len(M) - 1, len(M[0]) - 1)

    Метод read_maze_from_file() считывает текстовый файл с определением лабиринта и возвращает соответствующий ему список списков. БОльшую часть кода занимает итерационная функция draw_maze(), которая рисует лабиринт, используя пакет Matplotlib. В последних строках кода лабиринт считывается из файла и рисуется, если путь от его начальной (верхней левой) до конечной (нижней правой) клетки найден.

    Результат работы приложения приведен на рисунке 4.

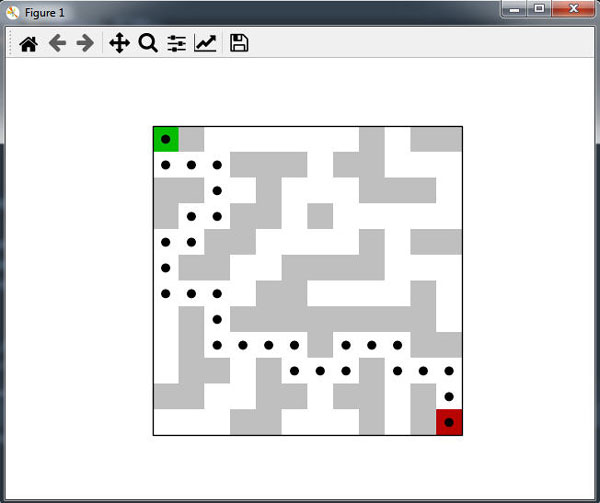
Рис.4. Результат работы приложения

    На следующем шаге мы рассмотрим судоку.

Предыдущий шаг Содержание Следующий шаг