На этом шаге мы введем пространство состояний сети Петри.

Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети Петри. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т.е. Nⁿ. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения b, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке m (состоянию) и переходу t_j, она образует новую маркировку (состояние), которая получается при запуске перехода t_j в маркировке m. Так как t_j может быть запущен только в том случае, когда он разрешен, то функция b(m, t_j) не определена, если t_j не разрешен в маркировке m. Если же t_j разрешен, то b(m, t_j) = m', где m' есть маркировка, полученная в результате удаления фишек из входов t_j и добавления фишек в выходы t_j.

Пусть дана сеть Петри C = (P, T, I, O) с начальной маркировкой m⁰. Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода t_j в начальной маркировке образует новую маркировку m¹ = b( m⁰, t_j). В этой новой маркировке можно запустить любой другой разрешенный переход, например, t_k, образующий новую маркировку m² = b(m¹, t_k). Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.

При выполнении сети Петри получаются две последовательности: последовательность маркировок ( m⁰, m¹, m², …) и последовательность переходов, которые были запущены (t_j0, t_j1, t_j2, ...). Эти две последовательности связаны следующим соотношением: b(m^k, t_jk) = m^k+1 для k = 0, 1, 2, ... . Имея последовательность переходов и m⁰, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Обе эти последовательности представляют описание выполнения сети Петри.

Пусть некоторый переход в маркировке m разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке m есть новая маркировка m'. Говорят, что m' является непосредственно достижимой из маркировки m, если существует переход t_j, принадлежащий T, такой, что b(m, t_j) = m'.

Определение.: Для сети Петри C = (P, T, I, O) с маркировкой m маркировка m' называется непосредственно достижимой из m, если существует переход t_j, принадлежащий T, такой, что b (m, t_j) = m'.

Можно распространить это понятие на определение множества достижимых маркировок данной маркированной сети Петри. Если m' непосредственно достижима из m, а m'' - из m', говорят, что m'' достижима из m'. Определим множество достижимости R(C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m' принадлежит R(C, m), если существует какая-либо последовательность запусков переходов, из меняющих m на m'.

Определение.

Множество достижимости R(C, m) для сети Петри C = (P, T, I, O) с маркировкой m есть наименьшее множество маркировок, определенных следующим образом:

m принадлежит R(C, m) ;
Если m' принадлежит R(C, m) и m'' принадлежит b(m', t_j) для некоторого t_j, принадлежащего T, то, m'' принадлежит R(C, m) .

Для сети Петри, изображенной на рисунке 1, и маркировки m = (1, 0, 0) непосредственно достижимыми являются две маркировки: (0, 1, 0) и (1, 0, 1). Из (0, 1, 0) нельзя достичь ни одной маркировки, так как ни один переход не разрешен. Из (1, 0, 1) можно получить (0, 1, 1) и (1, 0, 2).

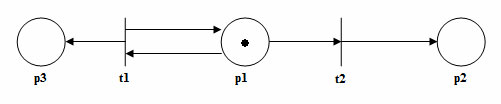
Рис.1. Маркированная сеть Петри

Со следующего шага мы начнем рассматривать использование сетей Петри для моделирования.

Предыдущий шаг Содержание Следующий шаг