На этом шаге мы кратко опишем некоторые модификации сетей Петри.
Сети Петри могут быть использованы для моделирования самых различных систем, в том числе аппаратного и программного обеспечения ЭВМ. Очевидно, что сети Петри могут адекватно моделировать разные системы, однако могут существовать такие системы, которые нельзя должным образом моделировать сетями Петри, т. е. мощность моделирования сетей Петри имеет пределы.
Применение классических подходов и добавление дополнительных атрибутов позволили разработать сети различной целевой направленности, получившие название расширенные. Классификация расширенных сетей Петри приведена на рисунке 1.
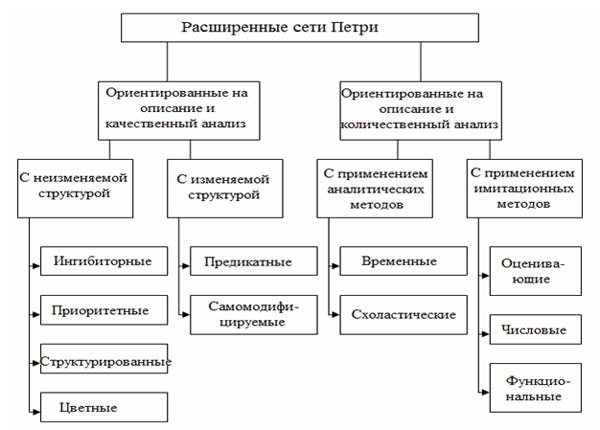
Рис.1. Виды расширенных сетей Петри
Рассмотрим подробнее некоторые типы сетей Петри.
Ингибиторная сеть представляет собой сеть Петри, дополненную специальной функцией инцидентности IIN: Р х Т -> {0, 1}, которая вводит ингибиторные (запрещающие) дуги для тех пар (p, t), для которых IIN(Р, Т) = 1. Ингибиторные дуги связывают только позиции с переходами, на рисунках их изображают заканчивающимися не стрелками, а маленькими кружочками.
Переход t в ингибиторных сетях может сработать, если каждая его входная позиция, соединенная с переходом обычной дугой с кратностью w(p, t) содержит не менее w(p, t) фишек, а каждая входная позиция, соединенная с переходом t ингибиторной дугой (ее кратность всегда равна 1), имеет нулевую разметку.
Например, используя ингибиторную дугу, можно промоделировать оператор условного вычитания (если xi<>0, то xi = xi- 1) и получить фрагмент ингибиторной сети (рисунок 2).
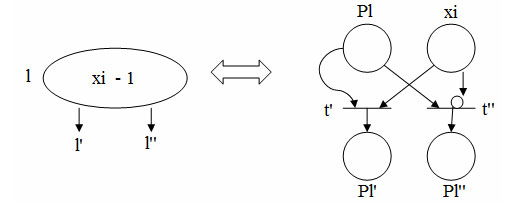
Рис.2. Фрагмент ингибиторной дуги
Ингибиторные сети используются для разработки диагностических моделей средств вычислительной техники.
В приоритетных сетях вводят приоритеты срабатывания переходов. Если несколько переходов являются разрешенными, то срабатывает тот из них, который имеет наивысший приоритет. Такие сети используются для моделирования систем на уровне задач.
В структурированных сетях некоторые из переходов являются сложными. При их срабатывании запускается сеть другого уровня иерархии (рисунок 3).
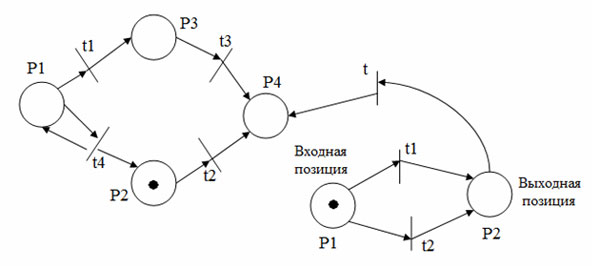
Рис.3. Структурированная сеть Петри
Срабатывание t2 приводит к запуску сети другого уровня. Выполнение сложного перехода заключается в помещении во входную позицию по сети фишки. После выполнения сети фишка появляется в ее выходной позиции, затем формируются фишки в выходных позициях сложного перехода.
Преобразование сети к виду, имеющему один вход и один выход, всегда возможно. Такие сети используются для моделирования модульных вычислительных систем.
В цветных сетях вводится понятие цвета для фишек. В общем случае может быть n цветов. В вычислительной технике используются трехцветные сети (n = 3). Такие сети используются для моделирования аппаратных средств.
В сетях с изменяемой структурой кратность ребер не является постоянной.
В самомодифицируемых сетях кратность ребра может задаваться либо натуральным числом N, либо определяться количеством фишек, находящихся во входных позициях некоторого перехода.
Качественными характеристиками могут быть: отсутствие зацикливаний в системе, достижение некоторого состояния системы (например, конечного).
Количественными характеристиками являются: время работы некоторого маршрута в программе, время прохождения сигнала в схеме и т. д.
Во временных сетях переходам ставится в соответствие их времена срабатывания, либо позициям ставится в соответствие времена нахождения фишек в позициях.
В стохастических сетях указанные характеристики являются вероятностными, т. е. вводится функция плотности вероятности времен срабатывания переходов или времен нахождения фишек в позициях.
Предикатные сети - это сети с логическим описанием состояния системы.
Со следующего шага мы начнем рассматривать созданное приложение "Редактор сетей Петри" для моделирования систем.
