На этом шаге мы рассмотрим свойство сохраняемости сети Петри.
Сети Петри можно использовать для моделирования систем распределения ресурсов. Например, сеть Петри может моделировать запросы распределения и освобождения устройств ввода-вывода в вычислительной системе. В этих системах некоторые функции могут представлять ресурсы. Группа из трех построчно печатающих устройств представляется позицией, имеющей в начальной маркировке три фишки. Запрос построчно-печатающего устройства - это переход, для которого данная позиция является входной; затем устройство освобождается переходом, для которого позиция построчно печатающих устройств является выходной.
Сети Петри такого типа должны обладать свойством живучести или сохранения. Для этого фишки, представляющие ресурсы, не должны создаваться или уничтожаться, общее число фишек в сети должно оставаться постоянным.
- Определение.
- Сеть Петри С = (Р, Т, I, О) с начальной маркировкой m называется строго сохраняющей, если для всех m' принадлежащих
R(C, m):
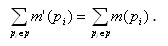
Строгое сохранение требует, чтобы число входов в каждый переход должно равняться числу выходов |I(tj)| = |O(tj)|. Если это условие не будет выполняться, то запуск перехода изменил бы число фишек в сети.
Рассмотрим график сети Петри (рисунок 1), которая не является строго сохраняющей.
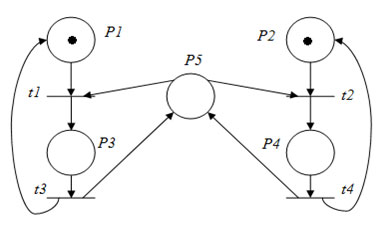
Рис.1. Сеть Петри, не являющаяся строго сохраняющей
В этой сети запуск перехода t1 или t2 уменьшает число фишек на 1, а запуск переходов t3 или t4 добавит фишку к маркировке. Эту сеть можно преобразовать в сеть строго сохраняющую (рисунок 2).
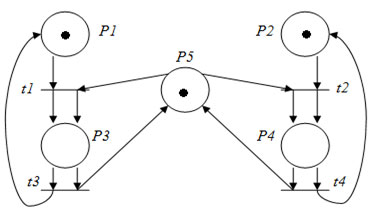
Рис.2. Строго сохраняющая сеть Петри
Сеть Петри должна сохранять ресурсы, которые она моделирует. Однако взаимно однозначного соответствия между фишками и ресурсами нет.
Фишка может представлять собой один программный счетчик или какой-нибудь другой элемент или несколько ресурсов сразу. В этом случае фишка используется для создания кратных фишек путем запуска перехода с большим числом выходов, чем входов.
В общем случае следует определить взвешивание фишек. Взвешенная сумма для всех маркировок должна быть постоянной. Фишкам, не являющимся важными, можно присвоить вес 0; другим фишкам можно присвоить веса 1, 2, 3 или другое целое число. Фишка определяется ее позицией в сети. Следовательно, веса связаны с каждой позицией сети.
Вектор взвешивания w = (w1, w2, ..., wn) определяет вес wi для каждой позиции pi, принадлежащей Р.
- Определение.
- Сеть Петри С = (P, T, I, O) с начальной маркировкой m называется сохраняющей по отношению к вектору взвешивания w, где
w = (w1, w2, ..., wn), при n = | P |, wi > 0, если для всех
m', принадлежащих R(C, m):
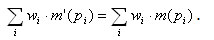
Строго сохраняющая сеть Петри является сохраняющей по отношению к вектору взвешивания (1, 1, ..., 1). Все сети Петри являются сохраняющими по отношению к вектору взвешивания (0, 0, ..., 0).
На следующем шаге мы рассмотрим активность сети Петри.
