На этом шаге мы рассмотрим алгоритм отыскания компонент сильной связности в орграфе.

    Пусть G = (V, Е) - связный орграф. Алгоритм 1 легко приспособить для организации поиска в глубину в орграфе G. Для этого нужно лишь список list(v) заменить списком list(v'), состоящим из концов всех дуг, выходящих из вершины v. Все понятия, связанные с поиском в глубину в обыкновенном графе, очевидным образом применимы и для орграфов. В частности, в результате поиска в глубину в орграфе G строится d-лес (глубинный лес), состоящий из ориентированных корневых деревьев. Тем самым, на множестве вершин орграфа G вводится отношение частичного порядка: u < v, если u, v принадлежат одной компоненте связности d-леса и u является потомком v. Отметим также, что поиск в глубину разбивает множество всех дуг орграфа на четыре класса:

1. древесные дуги, идущие от отца к сыну;
2. обратные дуги, идущие потомка к предку;
3. прямые дуги, идущие от предка к потомку, но не являющиеся древесными дугами;
4. поперечные дуги, соединяющие вершины, ни одна из которых неявляется потомком другой.

    На рисунке 1 показан орграф и его глубинный лес.

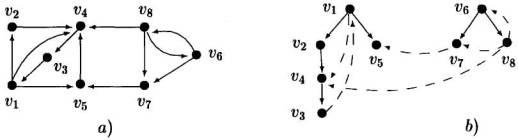
Рис.1. Ортграф и глубинный лес

    Следующие два утверждения очевидны.

Лемма 1.

Если vu - поперечная дуга графа G, то num[u] < num[v].

Лемма 2.

Пусть u, v, w - такие вершины орграфа G, что num[u] < num[v] < num[w] и w является потомком u. Тогда вершина v - потомок вершины u.

    Применим поиск в глубину для построения алгоритма, способного распознавать сильную связность орграфа G. На самом деле будет построен алгоритм, который сможет в орграфе G выделять компоненты сильной связности, являющиеся максимальными сильно связными подграфами орграфа G. Заметим, что компоненты сильной связности являются классами отношения взаимной достижимости на множестве вершин орграфа G.

    Пусть G_i = (V_i E_i) (1 ≤ i ≤ k) - компоненты сильной связности орграфа G. Обозначим через r_i такую вершину компоненты G_i (1 ≤ r ≤ k), что num[r_i] = min num(v_i). Пусть r - преобразование множества вершин орграфа G, определенное правилом: r(w) = r_i для любой вершины w ∈ G_i. Ясно, что вершины u и w лежат в одной компоненте сильной связности тогда и только тогда, когда r(u) = r(w).

Лемма 3.

Если w ≠ r(w), то w < r(w).

Доказательство.

Поскольку r(w) и w взаимно достижимы, существует кратчайшая (r(w), w)-орцепь P длины q > 1. Проведем индукцию по q.

    Пусть q = 1. Тогда существует дуга r(w)w. Ясно, что эта дуга древесная или прямая, поэтому w - потомок r(w).

    Допустим, что q > 1. Обозначим через х предпоследнюю вершину орцепи Р. Легко проверяется, что вершины х и r(w) взаимно достижимы, поэтому х и r(w) лежат в одной компоненте сильной связности. Следовательно, к вершине х применимо предположение индукции. Таким образом, вершина х - потомок r(w). Если xw - древесная или прямая дуга, то w < х и потому r < r(w). Пусть xw является обратной или поперечной дугой. Применяя лемму 1, получаем, что num[w] < num[х]. Так как num[r(w)] < num[w] и x - потомок r(w), вершины r(w), w, х удовлетворяют условиям леммы 2, т.е. w < r(w).

Лемма 4.

Пусть u - произвольная вершина, удовлетворяющая неравенствам r(w) > u > w. Тогда r(u) = r(w).

Доказательство.

Поскольку r(w)>u> w, существует (r(w), w)-opцепь Р, проходящая через вершину u. Кроме того, r(w) достижима из w. Следовательно, r(w) и u взаимно достижимы, т.е. r(u) = r(w).

    Пусть v - произвольная вершина орграфа G. Через v обозначим поддерево d-леса с корнем v. Если X ⊆ v, то множество всех таких вершин w, что r(w) > v и для некоторой вершины х ∈ X существует обратная или поперечная дуга xw, будем обозначать, как и раньше, через VB(X, v).

    Леммы 3 и 4 показывают, что вершины каждой компоненты сильной связности d, 1 ≤ i ≤ k, образуют в глубинном лесе поддерево с корнем r_i.

Лемма 5.

Пусть v и w - такие вершины графа G, что w ∈ VB(v, v). Тогда r(w) = r(v).

Теорема 4.

Пусть v - произвольная вершина орграфа G. Равенство v = r(v) выполнено тогда и только тогда, когда VB(v, v) ⊆ v.

Доказательство.

Пусть v - такая вершина, что v - r(v). Возьмем произвольную вершину w ∈ VB(v, v). В силу леммы 5 имеем r(w) = r(v) = v. Отсюда с учетом леммы 3 получаем, что w ∈ v.

    Предположим, что v ≠ r(v). Из леммы 3 следует, что v < r(v). С другой стороны, существует (v, r(v))-орцепь Р. В орцепи P найдем первую дугу xw такую, что w не принадлежит v. Очевидно, xw - обратная или поперечная дуга. Кроме того, легко проверяется, что w и v лежат в одной компоненте сильной связности орграфа G. Следовательно, r(w) = r(v) > v. Таким образом, w ∈VB(v, v), откуда вытекает, что VB(v, v) ⊆ v.

    На множестве V вершин графа G рассмотрим следующую функцию

L[v] = min num({v} ∪ VB(v, v)).

Теорема 5.

Пусть v - произвольная вершина орграфа G. Равенство v = r(v) выполнено тогда и только тогда, когда L[v] = num[v].

Доказательство.

Пусть v = r(v). Тогда VB(v, v) ⊆ v. Поэтому min num(VB(v,v)) ≤ num[v]. Отсюда L[v] = num[v].

    Предположим, что v ≠ r(v). Учитывая теорему 4, получаем, что существует w ∈ VB(v, v)\v. Найдется такая вершина w ∈ v, что xw - обратная или поперечная дуга. Следовательно, num[w] < num[х]. Проверим, что num[w] < num[v]. Рассуждая от противного, допустим, что num[v] ≤ num[w]. Поскольку w ≠ v, имеем строгое неравенство num[v] < num[w]. К вершинам v, w, x можно применить лемму 2, поэтому w ∈ v, что невозможно. Из доказанного неравенства следует, что L[v] < num[w] < num[v].

    Теорема 5 позволяет распознавать в каждой компоненте сильной связности вершины v, удовлетворяющие условию v = r(v). Сравнивая теорему 5 с теоремой 2, мы видим, что роль таких вершин для орграфов аналогична роли точек сочленения для обыкновенных графов.

Лемма 6.

Пусть v - произвольная вершина орграфа G. Тогда L[v] = min(num[v], L[s₁], ..., L[s_p], num(VB(v, v))), где s₁, ..., s_p - все сыновья вершины v.

    Перейдем к описанию алгоритма, позволяющего строить компоненты сильной связности орграфа G. Пусть к орграфу применен поиск в глубину. В компонентах сильной связности G_i, 1 ≤ i ≤ k, ранее были выделены корневые вершины r_i. С этого момента будем считать, что компоненты сильной связности занумерованы следующим образом: если 1 ≤ i < j ≤ k, то вершина r_i использована поиском в глубину раньше, чем вершина r_j. Такая нумерация компонент сильной связности обладает следующим важным свойством.

Лемма 7.

Компонента сильной связности G_i, 1 ≤ i ≤ k, совпадает с множеством всех элементов из поддерева, не принадлежащих компонентам G₁, ..., G_i-1.

    Из леммы 7 легко извлекается следующий способ нахождения компонент сильной связности. Определим стек S и будем помещать в него вершины орграфа G в том порядке, в каком их просматривает поиск в глубину. Если сразу после того, как вершина г_i использована, вытолнуть из стека S все вершины до r_i включительно, мы получим компоненту G_i.

    Теперь мы можем привести формальное описание алгоритма для отыскания компонент сильной связности орграфа G.

    Алгоритм 3.

1. procedure StrongComp(v);
2. begin
3.   num[v]:= i; L[v]:= i; i:= i+1; S <= v;
4.   for w ∈  do
5.      if num[w] = 0 then
6.              begin
7.                StrongComp(w); L[v]:= min(L[v], L[w]);
8.              end
9.    else if num[w] < num[v] and w ∈ S then
10.            L[v]:= min(L[v], num[w]);
11.   if L[v] = num[v] then
12.   while num[top(S)] ≥ num[v] do
13.     begin
14.       x <= S; {добавить x к очередной компоненте сильной связности;}
15.     end
16. end;
17. begin
18.   i:= 1; S:= nil;
19.   for v ∈ V do num[v]:= 0;
20.   for v ∈ V do
21.     if num[v] = 0 then StrongComp(v)
22. end.

    Процедура StrongComp(v) является модифицированной версией рекурсивной процедуры DFS(v) алгоритма 1. Для данной вершины v значение функции L[v] вычисляется циклом в строках 4-10 в соответствии с формулой, полученной в лемме 6. В строке 11 для вершины r проверяется условие из теоремы 5, означающее, что v - корневая вершина очередной компоненты сильной связности. Для нахождения компонент сильной связности использован упомянутый выше стек S, элементами которого являются вершины орграфа G (строки 12-15). Кроме того, этот стек участвует в формировании условия, проверяемого в строке 9. Выполнение этого условия означает, что w ∈ VB(v, v).

    Мы изложили неформальные соображения по поводу правильности работы алгоритма 3. Перейдем к строгим рассуждениям.

Теорема 6.

Алгоритм 3 правильно строит компоненты сильной связности орграфа G.

Доказательство.

Занумеруем компоненты сильной связности G_i, 1 ≤ i ≤ k, в порядке использования корневых вершин r, поиском в глубину. В силу леммы 7 множество вершин V₁ компоненты G₁ совпадает с множеством r₁, состоящим из вершины r₁ и всех ее потомков. В процессе работы процедуры StrongComp(r₁) происходят обращения к процедуре StrongComp(u) для каждого из потомков вершины r₁. Проверим, что ни в одной из этих процедур равенство L[u] = num[u] не выполнено (здесь и далее речь идет о значениях функции L, вычисленных алгоритмом 3). Полагая противное, можно выбрать среди вершин, для которых равенство выполнено, минимальную вершину x (напомним, что d-лес является частично упорядоченным множеством). Ясно, что х ≠ r(х) =r₁. Из теоремы 4 вытекает, что VB(x, x) ⊆ х. Поэтому существует обратная или поперечная дуга yz, где у ∈ х. С использованием леммы 3 нетрудно проверить, что num[z] < num[x]. Выбор вершины х гарантирует, что все вершины, просмотренные поиском в глубину, содержатся в стеке S. Следовательно, при выполнении процедуры StrongComp(x) условие в строке 9 (считая, что w = z) выполнится. Поэтому текущее значение L[x] не превосходит num[z] < num[x]. Отсюда следует, что значение L[x], подсчитанное процедурой, будет меньше чем num[x]. Это противоречит выбору x.

    Покажем, что в процессе выполнения процедуры StrongComp(r₁) условие L[r₁] = num[r₁] будет выполнено. Напомним, что множество r₁ совпадает с множеством вершин компоненты G₁. Отсюда следует, что VB(u, u) ⊆ VB(r₁, r₁) для любого потомка u вершины r₁. Из теоремы 4 вытекает, что VB(r₁, r₁) ⊆ r₁. При выполнении процедуры StrongComp(u) все просмотренные вершины находятся в стеке S. Поэтому значения L[u], уточняемые в строках 7 и 10, всегда будут не меньше, чем num[r₁]. С учетом присваиваний в строке 3, имеем L[r₁] = num[r₁].

    Для завершения доказательства применим индукцию по числу q компонент сильной связности орграфа G.

    Пусть q = 1. Тогда G = G₁, т. е. все вершины орграфа G, отличные от вершины r₁, являются ее потомками. Условие в строке 11 выполнится только один раз при v = r₁. Поэтому из стека S будут вытолкнуты все вершины орграфа G.

    Предположим, что q > 1. Пусть алгоритм 3 начинает работу с вершины v₀. В процессе работы алгоритма после завершения работы процедуры DFS(r₁) из стека S будут вытолкнуты все вершины компоненты сильной связности G₁. Обозначим через G' подграф, полученный из орграфа G удалением компоненты d. Очевидно, к орграфу G' применимо предположение индукции. Следовательно, все компоненты, отличные от G₁, будут найдены правильно.

    На следующем шаге мы рассмотрим поиск в ширину.

Предыдущий шаг Содержание Следующий шаг