На этом шаге мы рассмотрим полумодулярные решетки, условие Жордана - Дедекинда.

    Напомним, что решеткой называется алгебра L с двумя бинарными операциями ∧ и ∨ такими, что для любых а, b, с ∈ L выполняется

1) а ∧ а = а,                    1') а ∨ а = а,

2) а ∧ b = b ∧ а,                2') а ∨ b = b ∨ а,

3) а ∧ (b ∧ с) = (а ∧ b) ∧ с,    3') a ∨ (b ∨ c) = (a ∨ b) ∨ c,

4) а ∧ (а ∨ b) = а,              4') а ∨ (а ∧ b) = а.

    В решетке L можно ввести отношение частичного порядка ≤, полагая

a ≤ b ⇔ a ∧ b = a (a, b ∈ L).

    Отметим, что a ∧ b и a ∨ b являются соответственно точной нижней и точной верхней границами для элементов а и b относительно ≤. Решетка L называется модулярной, если

а ≥ b → a ∧ (b ∨ с) = b ∨ (a ∧ с)

для любых а, b, с ∈ L.

    Для элементов а и b решетки L таких, что a ≤ b, положим

[а, b] = {x | а ≤ x ≤ b}.

    Это подмножество замкнуто относительно операций ∨ и ∧, т.е. является подрешеткой, и называется интервалом решетки L.

Лемма 1.

Для любых элементов а и b модулярной решетки L интервалы [а ∧ b, а] и [b, а ∨ b] изоморфны.

Доказательство.

Определим отображение φ из [а ∧ b, а] в [b, а ∨ b] и отображение ψ из [b, а ∨ b] в [а ∧ b, а], полагая

φ(х) = x ∨ b (x ∈ [а ∧ b, а]),
ψ(y) = y ∧ b (y ∈ [b, а ∨ b]),

    Заметим, что

a ∧ b ≤ x ≤ a => b=(a ∧ b) ∨ b ≤ φ(x) ≤ а ∨ b

и

b ≤ y ≤ a ∨ b => a ∧ b ≤ ψ(y) ≤ а ∧ (а ∨ b) = а.

    Далее, для любого х ∈ [а ∧ b, a] выполняется

ψφ(x) = (x ∨ b) ∧ а = x ∨ (а ∧ b) = x,

т.е. ψφ тождественно на [а ∧ b, а] и, аналогично, ψφ тождественно на [b, а ∨ b]. Следовательно, ψ и φ - две взаимно обратные биекции. Кроме того, ψ и φ сохраняют отношение ≥:

x₁ ≤ x₂ = φ(х₁) ≤ φ(х₂), у₁ ≤ y₂ => ψ(y₁) ≤ ψ(y₂)

для любых x₁, x₂ ∈ [а ∧ b, а], y₁, y₂ ∈ [b, a ∨ b].

    Отсюда следует, что φ - изоморфизм подрешетки [a ∧ b, а] на подрешетку [b, а ∨ b].

    Через <• будем обозначать в решетке L отношение покрытия, т.е. мы полагаем а<•b, если а < b и интервал [а, b] двухэлементен.

    Решетка L называется полумодулярной, если

a ∧ b <• а => b <• а ∨ b

для любых а, b ∈ L. В силу леммы 1 любая модулярная решетка полумодулярна.

    Пусть V - конечномерное векторное пространство над телом F. Тогда решетка Sub V подпространств пространства V, как известно, модулярна и, следовательно, полумодулярна.

    Рассмотрим теперь решетку L, в которой все цепи конечны. Будем говорить, что L удовлетворяет условию Жордана-Дедекинда, если для любых двух элементов а, b ∈ L таких, что а<b, все максимальные (а, b)-цепи в L имеют одинаковую длину, т. е. всегда из условий

а = u₀ <• u₁ <• ... <• u_m = b, а = v₁ <• v₂ <• ... <• v_n = b

вытекает m = n.

Теорема 1.

Любая полумодулярная решетка, в которой все цепи конечны, удовлетворяет условию Жордана-Дедекинда.

Доказательство.

Будем доказывать следующее утверждение: для любых а, b ∈ L таких, что а < b, если какая-либо максимальная (а, b)-цепь имеет длину m, то любая максимальная (а, b)-цепь имеет длину m.

    При m = 1 имеем а <• b и утверждение очевидно.

    Пусть утверждение верно для любого интервала, имеющего максимальную цепь длины меньшей m, и m ≤ 2. Рассмотрим две максимальные (а, b)-цепи: а = u₀ <• u₁ <• ... <• u_m = b, а = v₁ <• v₂ <• ... <• v_n = b.

    В силу предположения индукции мы можем считать, что m > n. Если u₁ = v₁, то, применяя предположение индукции к интервалу [u₁, b], получаем m - 1= n - 1, т. е. m = n. Пусть u₁, v₁ <• u₁∨ v₁. В силу полумодулярности выполняется u₁, v₁ <• u₁. По предположению индукции любая максимальная (u₁, b)-цепь имеет длину m - 1. Следовательно, любая максимальная (u₁ ∨ v₁, b)-цепь имеет длину m-2. Отсюда следует, что любая максимальная (v₁, b)-цепь имеет длину m - 1. Тогда m - 1 = n - 1, т.е. опять имеем m = n.

    Далее под отношением <• на решетке L будем понимать объединение отношения покрытия <• и отношения равенства =. В дальнейшем мы будем рассматривать решетки, обладающие наименьшим элементом, который будем называть нулем и будем обозначать через 0. Атомом будем называть элемент решетки, покрывающий ее наименьший элемент 0.

Лемма 2.

Пусть L - полумодулярная решетка с нулем 0. Тогда для любых u, v, w ∈ L выполняется,

u <• v > u ∨ w ≤ v ∨ w.

    В частности, для любого а ∈ L и атома р такого, что р не находится в отношении частичного порядка с а, выполняется

а <• a ∨ р.

Доказательство.

Если v ≤ u ∨ w, то u ∨ w = (u ∨ w) ∨ v = v ∨ w. Пусть v не находится в отношении частичного порядка u ∨ w. Тогда u = w ∧ (u ∨ w), так как u <• v, и v ∨ (u ∨ w) = v ∨ w. Отсюда в силу полумодулярности получаем u ∨ w <• v ∨ w.

    Пусть L - полумодулярная решетка с нулем 0, в которой все цепи конечны. Через dim а будем обозначать длину максимальной (0, a)-цепи. Это определение корректно в силу теоремы 1. Функцию dim x будем называть функцией размерности на решетке L.

Теорема 2.

Пусть L - полумодулярная решетка с нулем 0, в которой все цепи конечны. Тогда

1. для любых a, b ∈ L

   dim(a ∧ b) + dim (a ∨ b) ≤ dim a + dim b;

2. решетка L модулярна в том и только в том случае, когда для любых a, b ∈ L

   dim(a ∧ b) + dim(a ∨ b) = dim a + dim b.

Доказательство.

1. Пусть a∧b - u₁ <• u₂ <• ... <• u_m = u. Объединяя все элементы этой цепи с b, в силу леммы 2 получаем

   b = u₀ ∨ b ≤• u₁ ∨ b ≤• ...≤• u_m ∨ b = a ∨ b.

       Отсюда следует dim а - dim(a ∧ b) = b ≥ dim(a ∨ b) - dim b,

   т.е.

   dim a + dim b ≥ dim(a ∧ b) + dim(a ∨ b).

2. Если решетка модулярна, то интервалы [а ∧ b, a] и [b, а ∨ b] изоморфны по лемме 1. Следовательно,

   dim a - dim(a ∧ b) = dim(a ∨ b) - dim b.

       Обратно, предположим, что для любых а, b ∈ L выполняется равенство

   dim(a ∧ b) + dim(a ∨ b) = dim a + dim b.

       Пусть, от противного, решетка L немодулярна. Тогда, как известно, она содержит Пентагон (рис. 1) в качестве подрешетки.

   
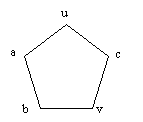
   Рис.1. Пентагон

       Для элементов Пентагона в силу нашего предположения получаем

   dim v + dim u = dim с + dim a,

   dim v + dim u = dim с + dim b,

   т. е. dim a = dim b, что невозможно.

    Отметим, что неравенство из 1) называют неравенством полумодулярности.

    На следующем шаге мы рассмотрим конечномерные геометрические решетки и матроиды.

Содержание Следующий шаг