Шаг 2.
Матроиды. "Жадные" алгоритмы.
Конечномерные геометрические решетки и матроиды

    На этом шаге мы рассмотрим конечномерные геометрические решетки и матроиды.

    Неодноэлементную решетку L называют конечномерной геометрической решеткой, если она

1. полна, т. е. существуют точная нижняя и точная верхняя границы любого множества ее элементов;
2. не содержит бесконечных цепей;
3. точечна, т. е. любой её элемент представим в виде объединения некоторого (возможно бесконечного) множества атомов;
4. полумодулярна.

    Заметим, что в силу 2) решетка L имеет наименьший и наибольший элементы, которые удобно считать соответственно точной верхней и точной нижней границей пустого множества.

    Примером конечномерной геометрической решетки может служить решетка подпространств Sub V любого конечномерного векторного пространства V над телом F.

    Решетка L называется решеткой с дополнениями, если она имеет наименьший элемент 0, наибольший элемент 1 и для любого u ∈ L существует v ∈ L такой, что

u ∧ v = 0, и u ∨ v = 1.

    Элемент v называют тогда дополнением элемента u.

    Решетка называется решеткой с относительными дополнениями, если любой ее интервал есть решетка с дополнениями.

Теорема 3.

Любая конечномерная геометрическая решетка является решеткой с относительными дополнениями.

Доказательство.

Пусть [а, b] - интервал конечномерной геометрической решетки L и u ∈ [а, b]. Среди элементов u' ∈ [а, b] таких, что u ∧ u' = а (отметим, что это равенство верно при u' = а), возьмем максимальный элемент u'. Покажем, что u ∨ u' = b, т. е. u' - дополнение для u.

    Пусть, от противного, u ∨ u' < b. Возьмем атом q ≤ b решетки L такой, что q не находится в отношении частичного порядка с u ∨ u'. Такой атом существует в силу точечности решетки L. Тогда q не находится в отношении частичного порядка с u и q не находится в отношении частичного порядка с u'. Положим u''= u' ∨ q. Очевидно, а ≤ u' ∨ q ≤ b, т.е. u'' ∈ [а, b]. Так как q ≤ u', по лемме 2 получаем u' <• u' ∨ q = u''.

    В силу максимальности u' выполняется а < u ∧ u''. Тогда существует атом р ≤ u ∧ u'' ≤ u, u'' решетки L такой, что р не находится в отношении частичного порядка с а - u ∧ u'. Ясно, что р не находится в отношении частичного порядка с u', иначе из р ≤ u' и р ≤ u получаем р ≤ u ∧ u' = а. Так как р ≤ u'', отсюда следует u' <• u' ∨ р ≤ u'', т. е. u'' = u' ∨ р. Тогда получаем

q ≤ u'' ≤ u'' ∨ u = (u ∨ p) ∨ u = u ∨ (p ∨ u) = u' ∨ u,

что противоречит выбору q.

    Таким образом, u ∨ u' = b и u' - дополнение для u в [а, b].

Теорема 4.

Любой интервал конечномерной геометрической ре-шетки является конечномерной геометрической решеткой.

Доказательство.

Очевидно, нужно проверить лишь точечность интервала. Пусть в решетке L выполняется а < c ≤ b. Тогда с = для некоторых атомов р_i (i∈I) решетки L. Очевидно, среди указанных атомов существует такой атом p_i что p_i не находится в отношении частичного порядка с а. Будем считать, что р_j не находится в отношении частичного порядка с а для j ∈ J ⊆ I и p_k < а для k ∈ I\J. Тогда по лемме 2 предыдущего шага элементы p_j ∧ а являются атомами в интервале [а, b] для j ∈ J и

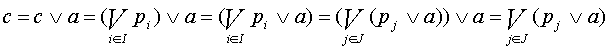
    Пусть Е - непустое множество. Отображение A → (А) множества P(E) всех подмножеств множества E в себя называется оператором замыкания, если для любых A, B ⊆ E выполняется

1. A ⊆ 〈А〉;
2. A ⊆ B => 〈А〉 ⊆ 〈B〉;
3. 〈〈А〉〉 = 〈А〉.

    Условие 1) называется направленностью, условие 2) - монотонностью, а условие 3) - идемпотентностью оператора замыкания. Подмножество А ⊆ Е называется замкнутым, если А = 〈А〉.

Лемма 1.

Пересечение любого семейства замкнутых подмножеств замкнуто.

Доказательство.

Пусть А_i (i ∈ I) - семейство замкнутых подмножеств. Тогда в силу монотонности

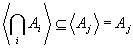
для любого j ∈ I.

    Отсюда получаем 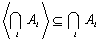, т.е. 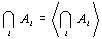в силу направленности оператора замыкания.

    Через Sub E обозначим множество всех замкнутых подмножеств оператора замыкания на Е. Ясно, что в силу направленности Е ∈ Sub E.

Следствие 1.

Sub E - полная решетка относительно ⊆.

Доказательство.

В Sub E существует точная нижняя граница для любого семейства элементов - это их пересечение, а также имеется наибольший элемент Е (удобно считать, что наибольший элемент есть пересечение пустого семейства элементов). Как хорошо известно, в таком случае частично упорядоченное множество является полной решеткой (т. е. существует и точная верхняя граница для любого семейства элементов).

    Заметим, что в Sub Е операции пересечения и объединения устроены следующим образом:

А∧В = А∩В и A∨В = A∪B.

---

    Пример. Пусть V - векторное пространство над телом F. Через 〈А〉 обозначим линейную оболочку множества А ⊆ V. Очевидно, А → 〈А〉 (А ⊆ V) - оператор замыкания на V, а решетка SubV подпространств пространства V и есть решетка замкнутых подмножеств.

    Матроидом или комбинаторной предгеометрией М(Е) называется непустое множество Е вместе с оператором замыкания А → 〈А〉 (А ⊆ Е) такое, что:

4. (аксиома замены) для любых p, q ∈ Е и А ⊆ Е из q ∉ 〈А〉 и q ⊆ (A ∪ p) вытекает p ⊆ (A ∪ q);
5. (аксиома существования конечного базиса) для любого А ⊆ Е существует такое конечное множество В ⊆ А, что 〈B〉 = 〈А〉.

    Матроид М(Е) называется простым или комбинаторной геометрией, если

6. 〈∅〉 = ∅ и 〈{p}〉 - {p} для любого p ∈ Е.

    В дальнейшем мы будем отождествлять множество {p} с его элементом p, что не вызовет недоразумений, и будем писать 〈p〉 = p.

    Замкнутые подмножества матроида М(Е) будем называть его листами или подпространствами. Ясно, что 〈∅〉 - наименьший лист в решетке листов Sub E матроида М(Е).

Лемма 2.

Пусть А - лист матроида М(Е) и p ∈ Е\А. Тогда А ⊂ 〈A∪p〉 в решетке Sub E листов матроида М(Е).

Доказательство.

Очевидно, А ⊂ 〈A∪p〉. Пусть В - такой лист, что А ⊂ В ⊆ (А∪p). Возьмем элемент q ∈ В\А. Тогда q ∉ А = 〈A〉 и q ∈ (А ∪ p). Откуда в силу аксиомы замены получаем р ∈ 〈A∪p〉 ⊆ В, т.е. A∪p ⊆ В. Следовательно, 〈A∪p〉 ⊆ В и поэтому В = 〈A∪p〉.

Следствие 2.

Если p ∈ Е\〈∅〉, то 〈p〉 - атом решетки Sub E.

Теорема 5 (Биркгоф и Уитни).

1. Решетка листов матроида является конечномерной геометрической решеткой.
2. Пусть L - конечномерная геометрическая решетка и Е - множество её атомов. Для каждого A ⊆ E положим

   〈A〉 = {p ∈ Е | p < ∨А}.

       Тогда множество Е вместе с отображением A → 〈A〉 является простым матроидом, решетка листов которого изоморфна L.

Доказательство.

1. Рассмотрим решетку Sub E листов некоторого матроида М(Е). В силу следствия 1 эта решетка полна. Она является точечной, так как

   A = ∨{〈p〉 | p ∈ A\ 〈∅〉}

   для любого А ∈ Sub E и по следствию 2 элементы 〈p〉, где p ∈ А\ 〈∅〉, есть атомы решетки Sub E.

       Покажем, что решетка Sub E полумодулярна. Пусть А, В - листы и А∩В ⊂ А. Возьмем элемент р ∈ А\(А∩В)=А\В. Тогда А =〈(А∩В) ∪ p〉. Отсюда получаем

   A ∨ B = 〈A ∪ B〉 = 〈B ∪ p〉

   и

   В ⊂ (B∪p)

   по лемме 2, т.е. В ⊂ А ∨ В.

       Проверим теперь, что Sub E не содержит бесконечных цепей.

       Покажем сначала, что Sub Е не имеет счетных возрастающих цепей, т.е. Sub E удовлетворяет условию обрыва возрастающих цепей. Пусть, от противного, А₁⊂ А₂⊂ ... - возрастающая цепь листов. В силу аксиомы существования конечного базиса существует конечное множество

   

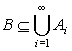
   такое, что

   

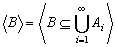
       В силу конечности В для некоторого j ∈ N выполняется В ⊆ A_j. Тогда

   

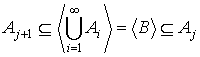
   что невозможно.

       Покажем теперь, что Sub E не имеет счетных убывающих цепей, т.е. Sub E удовлетворяет условию обрыва убывающих цепей. Пусть, от противного, А₁ ⊃ А₂ ⊃ ... - убывающая цепь листов. Для каждого i ∈ N выберем элемент a_i ∈ A_i\A_i+1 и положим А = {a₁, а₂, ...}. Положим также B_i = {a_i, a_i+1, ...} для любого i ∈ N. Поскольку 〈B_i+1〉 ⊆ A_i+1, для любого i ∈ N выполняется a_i ∉ (B_i+1).

       Предположим, что a_i ∈ 〈A\a_t〉 для некоторого t ∈ N. Тогда a_t ∈ 〈B_i\a_t〉 и a_t ∉ 〈B_t+1〉-(B_t\a_t) (здесь, очевидно, t ≠ 1). Отсюда следует, что существует j ∈ 1, ..., t-1 такое, что

   a_t ∈ 〈B_j \ a_i〉, a_t ∉ 〈B_j+1\ a_t〉.

       Преобразуя первое условие, получаем

   a_t ∈ 〈(B_j+1 ∪ a_j)\a_t〉 =〈(B_j+l\a_t)∪a_j〉.

       Теперь в силу аксиомы замены заключаем, что

   a_j ∈ 〈(B_j+1\a_t) ∪ a_t〉 = 〈B_j+1〉

   что невозможно.

       Мы установили, что a_t ∉ (А\a_t) для любого t ∈ N, но это противоречит аксиоме существования конечного базиса.

       Таким образом, Sub E удовлетворяет условию обрыва возрастающих цепей и условию обрыва убывающих цепей.

       Пусть Р - произвольная цепь из Sub E. В силу условия обрыва убывающих цепей в Р имеется наименьший элемент А₁. Если P\{А₁}≠∅, то в P\{A_i} имеется наименьший элемент А₂. Если P\{A₁, A₂}≠∅, то в P\{A₁, A₂} имеется наименьший элемент A₃. Продолжая этот процесс, мы будем строить возрастающую цепь А₁ ⊆ А₂ ⊆ А₃ ⊆ ... . В силу условия обрыва возрастающих цепей процесс построения возрастающей цепи завершится на некотором шаге, т. е. цепь P конечна.

       Итак, в решетке Sub E нет бесконечных цепей и мы завершили доказательство утверждения 1).

2. Легко проверить, что отображение А → 〈A〉 (А ⊆ Е) является оператором замыкания на множестве атомов Е конечномерной геометрической решетки L.

       Заметим также, что подмножество из Е замкнуто тогда и только тогда, когда оно состоит из всех атомов, лежащих под некоторым элементом решетки L.

       Покажем, что выполняется аксиома замены. Пусть q ∉〈А〉 и g ∈(A∪р) для некоторых p, q ∈ Е и А ⊆ Е. Тогда в решетке L имеем q не находится в отношении частичного порядка с ∨А и q ≤ (∨A) ∨ р. Из этих условий вытекает р не находится в отношении частичного порядка с ∨A. Тогда в силу полумодулярности и леммы 2 из предыдущего раздела получаем

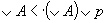   и

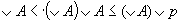
       Следовательно, (∨A)∨q = (∨А)∨р и поэтому р ≤ (∨A)Vg, т. е. р ∈〈A∪q〉. Проверим теперь аксиому существования конечного базиса. Пусть А ⊆ Е и А ≠ ∅. В интервале [0,∨А] будем строить возрастающую цепь. Пусть для некоторого I ∈ N уже построена цепь

   0 = u₀<•u₁<• ... <•u_i-1

   и u_i-1< ∨А. Очевидно, существует атом р_i ∈ А такой, что р_i не находится в отношении частичного порядка с u_i-1.

       Положим u_i = u_i-1∨ р. Ясно, что u_i-1 <• u_i ≤ ∨А, и мы получаем цепь

   0 = u₀<•u₁<• ... <•u_i-1<•u_i.

       Так как в решетке L нет бесконечных цепей, указанный процесс построения возрастающей цепи завершится на некотором шаге и мы получим цепь

   0 = u₀<•u₁<• ... <•u_n= ∨A.

   где n ∈ N. Положим В = {р₁, ..., р_n}. Мы имеем В ⊆ А и ∨A =u_n = u_n-1 ∨ p_n=u_n-2 ∨ p_n-1 ∨ p_n = ... = p₁ ∨ ... ∨ p_n = ∨B.

       Следовательно, 〈А〉 - 〈B〉 и мы проверили выполнение аксиомы существования конечного базиса.

       Итак, множество Е вместе с указанным оператором замыкания образует матроид. Поскольку

   〈∅〉 = {q ∈ Е | p ≤ ∨ ∅ = 0} = ∅,

   и

   〈p〉 = {q ∈ E | q ≤ p} = p,

   этот матроид является простым. Рассмотрим отображение f(u)={p ∈ E | p ≤ u} решетки L в решетку Sub E. Очевидно, это отображение сюрьективно. Оно инъективно, поскольку в силу точечности решетки L выполняется u = ∨ f(u) для любого u ∈ L. Следовательно, f - биекция L на Sub E. Если u₁ ≤ u₂ в L, то f(u₁) ⊆ f(u₂), и, обратно, если f(u₁) ⊆ f(u₂), то u₁=∨f(u₁)≤∨f(u₂) = u₂. Таким образом, f - изоморфизм решетки L на решетку Sub E.

    Заметим, что доказанная теорема говорит о том, что существует взаимно однозначное соответствие между конечномерными геометрическими решетками и простыми матроидами.

    В решетке Sub E₁ листов матроида М(Е) в силу ее полумодулярности и отсутствия бесконечных цепей определена функция размерности. Листы размерности 1, 2 и 3 будем называть соответственно точками, прямыми и плоскостями.

---

    Пример. Пусть V - n-мерное векторное пространство над телом F. Решетка Sub V подпространств пространства V является конечномерной геометрической решеткой, поэтому по теореме Биркгофа-Уитни ей отвечает некоторый простой матроид, который называют векторной проективной геометрией PG(n - 1, F) над телом F.

    В заключение этого шага обсудим без доказательства строение модулярных конечномерных геометрических решеток.

    Пусть U - некоторое непустое множество элементов, называемых точками, а £ - некоторое семейство подмножеств из U, называемых прямыми. Множество точек U и прямых £ называется проективной геометрией, если

1. через любые две различные точки проходит точно одна прямая;
2. любая прямая содержит не менее трех различных точек;
3. (аксиома Паша) если три точки а, b, с образуют треугольник, т. е. не лежат на одной прямой, и некоторая прямая l пересекает две стороны треугольника, но не в точках а, b, с, то она пересекает и третью сторону треугольника.

    Заметим, что доказанная теорема говорит о том, что существует взаимно однозначное соответствие между конечномерными геометрическими решетками и простыми матроидами.

    В решетке Sub E₁ листов матроида М(Е) в силу ее полумодулярности и отсутствия бесконечных цепей определена функция размерности. Листы размерности 1, 2 и 3 будем называть соответственно точками, прямыми и плоскостями.

---

    Пример. Пусть V - n-мерное векторное пространство над телом F. Решетка Sub V подпространств пространства V является конечномерной геометрической решеткой, поэтому по теореме Биркгофа-Уитни ей отвечает некоторый простой матроид, который называют векторной проективной геометрией PG(n - 1, F) над телом F.

    В заключение этого шага обсудим без доказательства строение модулярных конечномерных геометрических решеток.

    Пусть U - некоторое непустое множество элементов, называемых точками, а £ - некоторое семейство подмножеств из U, называемых прямыми. Множество точек U и прямых £ называется проективной геометрией, если

1. через любые две различные точки проходит точно одна прямая;
2. любая прямая содержит не менее трех различных точек;
3. (аксиома Паша) если три точки а, b, с образуют треугольник, т. е. не лежат на одной прямой, и некоторая прямая l пересекает две стороны треугольника, но не в точках а, b, с, то она пересекает и третью сторону треугольника.

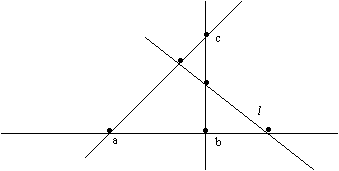
Рис.1. Пример решетки

    Подпространством А проективной геометрии называется такое её множество точек, которое вместе с любыми двумя различными точками из А содержит и прямую, проходящую через них.

    Введем понятие g-размерности или геометрической размерности для подпространств проективной геометрии. По определению точки имеют g-размерность 0, а прямые - g-размерность 1. Пусть А - произвольное подпространство g-размерности k и р - точка, не лежащая в А. Объединим все прямые, проходящие через р и точку из А. Получим, как нетрудно установить, подпространство. Это подпространство по определению имеет g-размерность k+1. Можно проверить, что понятие g-размерности введено корректно.

    Добавим к нашим трем аксиомам еще одну аксиому:

4. U имеет конечную g-размерность.

    Если U имеет g-размерность m, то говорят, что проективная геометрия (U, £) имеет g-размерность m.

    Пересечение любого семейства подпространств проективной геометрии, очевидно, является подпространством. Поэтому множество SubW всех подпространств проективной геометрии (U, £) является полной решеткой относительно теоретико-множественного включения. Нетрудно доказать следующее утверждение.

Теорема 6.

Sub U - модулярная конечномерная геометрическая решетка для любой проективной геометрии (U, £).

Теорема 7.

Любая проективная геометрия g-размерности m > 2 изоморфна векторной проективной геометрии PG(m, F) для некоторого тела F.

    Для проективных плоскостей, т. е. проективных геометрий g-размерности 2, справедлива следующая

Теорема 8.

Проективная плоскость изоморфна векторной проективной геометрии PG(2, F) для некоторого тела F тогда и только тогда, когда она удовлетворяет аксиоме Дезарга:

если два треугольника а1, а2, а3 и b1, b2, b3 перспективны относительно 
некоторой точки v (т. е. для любого i = 1, 2, 3 прямая, проходящая через 
аi, и bi, проходит и через v, то точки пересечения соответственных 
сторон треугольника лежат на некоторой прямой l (рис. 2).

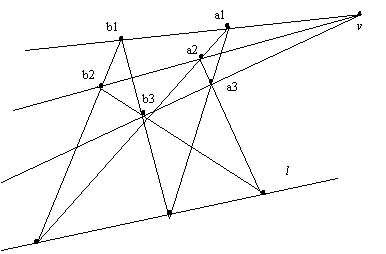
Рис.2. Иллюстрация к аксиоме Дезарга

    Заметим, что если для обычной евклидовой плоскости, во-первых, расширить множество точек, добавив семейство несобственных точек по одной для каждого пучка параллельных прямых, во-вторых, расширить каждую прямую, добавив несобственную точку пучка параллельных ей прямых, и, наконец, в-третьих, расширить множество прямых, добавив одну несобственную прямую, состоящую из всех несобственных точек, то получим дезаргову (т.е. удовлетворяющую аксиоме Дезарга) проективную плоскость. Рисунок 3 служит иллюстрацией для этого построения.

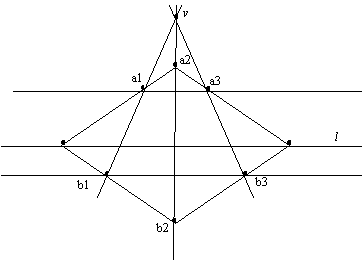
Рис.3. Иллюстрация построения

Теорема 9 (Биркгоф).

Модулярные конечномерные геометрические решетки исчерпываются прямыми произведениями конечного числа решеток вида Sub U для проективных геометрий (U, £).

    Отметим, что в силу предыдущих теорем фигурирующие здесь прямые множители Sub U представляют собой решетки подпространств конечномерных векторных пространств над телами, за исключением случаев, когда (U, £) - недезарговы проективные плоскости. К настоящему времени еще не получено полной классификации недезарговых проективных плоскостей.

    Отметим также, что дистрибутивные конечномерные геометрические решетки исчерпываются конечными булевыми алгебрами.

    Со следующего шага мы начнем рассматривать основные понятия теории матроидов.

Предыдущий шаг Содержание Следующий шаг