Шаг 4.
Матроиды. "Жадные" алгоритмы.
Различные аксиоматизации матроидов

    На этом шаге мы рассмотрим различные аксиоматизации матроидов.

Теорема 10 (Аксиомы независимости).

1) Пусть M(Е) матроид и Ind - семейство его независимых множеств. Тогда

    (I.1) Ind≠∅; X ⊆ J ∈ Ind влечет X ∈ Ind для любого X;

    (I.2) для любых I, J ∈ Ind таких, что |I| < |J|, существует p ∈ J\I, для которого I∪p ∈ Ind;

    (I.2') для любого A⊆Е все максимальные в A независимые подмножества равномощны.

    2) Обратно, пусть семейство I подмножеств конечного непустого множества Е удовлетворяет условиям (I.1), (I.2) или, что эквивалентно, условиям (I.1), (I.2'), где I играет роль Ind. Тогда I совпадает с семейством независимых множеств однозначно определенного матроида на Е.

Доказательство.

    1) Свойство (I.1) было уже отмечено в лемме 1 из предыдущего шага, а свойство (I.2') - в лемме 2. Применив (I.2') к I∪J, где I, J ∈ Ind и |I| < |J|, получим (I.2).

    2) Обратно, пусть I удовлетворяет условию (I.1), где вместо Ind фигурирует I. Легко видеть, что тогда (I.2) эквивалентно (I.2'). Поэтому будем считать, что выполняются все три свойства (I.1), (I.2) и (I.2').

    Общую мощность максимальных I-подмножеств из А назовем I-рангом множества A и обозначим через Ir(А). Зададим отображение A → 〈A〉 (А ⊆ Е), полагая для произвольного p ∪ Е: p ∪ 〈A〉 тогда и только тогда, когда p ∈ A или существует I ⊆ А такое, что I ∈ I и I∈p ∉ I.

    Заметим, что в силу леммы 5 предыдущего шага искомый оператор замыкания обязан быть таким.

    Свойства направленности и монотонности для заданного отображения очевидны.

    Прежде чем доказывать идемпотентность, покажем, что для любого A ⊆ E выполняется равенство

Ir(〈A〉)=Ir(A)

    Пусть, от противного, существуют такие I, J ∈ I, что I ⊆ A, J ⊆ 〈A〉 и

|I|=Ir(A)<Ir(〈A〉)=|J|

    Тогда в силу (I.2) найдется р ∈ J\I, для которого I∪p ∈ I. Учитывая максимальность I, получаем p ∈ 〈A〉\А. По определению 〈A〉 существует такое I' ⊆ A, что

I'∈ I, I'∪p ∉ I

    Очевидно, в силу (I.1) можно считать, что I' является максимальным I-множеством из А, т.е. |I'|=|I|. Тогда Ir(А) = |I'| < |I∪p|. По условию (I.2) существует q ∈ (I∪p)\I', для которого I'∪q ∈ I.

    Если q ∈ I, то I'∪q ⊆ A, что противоречит максимальности I'.

    Если q = р, то I'∪p ∈ I, что противоречит выбору множества I'.

    Таким образом, Ir(А) = Ir(〈А〉).

    Докажем идемпотентность нашего отображения, т.е. проверим, что 〈〈A〉〉 = 〈B〉 для любого А⊆Е.

    Пусть, от противного, существует p ∈ 〈〈〉〉\〈B〉. Возьмем некоторое максимальное I-множество B из А. Так как p ∉ 〈А〉, по определению замыкания 〈А〉 выполняется В∪p ∈ X. Следовательно,

Ir(〈А〉) = Ir(〈〈〉〉) ≥ |B∪p| = Ir(А)+1= Ir(〈А〉)+1,

что невозможно.

    Покажем теперь, что выполняется аксиома замены. Пусть A ⊆ Е, p, q ∈ Е, q ∉ 〈A〉 и q ∈ (A∪p). Тогда по определению замыкания существует I ∈ I, для которого I∪A∪p и I∪q ∉ I. Так как q ∉ 〈A〉, мы имеем

p ∈ I, (I\p)∪q ∈ I

    Положим I' = (I\p)∪q. Тогда I' ∈ I и I'∪p ∉ I, т. е. p ∈ 〈A∪q〉.

    Итак, наш оператор замыкания задает матроид М на Е.

    Наконец, А ∈ I выполняется тогда и только тогда, когда p ∈ 〈A\p〉. Для любого p ∈ A, что, в свою очередь, эквивалентно условию A ∈ Ind(M).

    Таким образом, I = Ind(M).

    Условия (I.1) и (I.2) называют аксиомами независимости.

Теорема 11 (Аксиомы баз).

1. Пусть M(Е) - матроид и Bs семейство его баз. Тогда:

       (B.1) Bs ≠∅; если В₁, В₂ ∈ Bs и В₁ ≠ В₂, то В₁ ⊄ В₂ и В₂ ⊄ В₁;

       (В.2) если В₁, В₂ ∈ Bs, то для любого b₁ ∈ В₁ существует b₂ ∈ В₂ такой, что (В₁\b₁)∪b₂ ∈ Bs.

2. Обратно, пусть семейство B подмножеств конечного непустого множества Е удовлетворяет условиям (В.1) и (В.2), где B играет роль Bs. Тогда B является семейством баз однозначно определенного матроида на Е.

Доказательство.

1. Свойство (В.1) очевидно, а свойство (В.2) вытекает из (I.2) и условия равномощности баз.
2. Обратно, пусть семейство B удовлетворяет аксиомам (В.1) и (В.2), где вместо Bs фигурирует B.

       Покажем сначала, что все B-множества равномощны. Пусть В₁, В₂ ∈ B. Без ограничения общности будем считать, что |B₁| ≤ |В₂|. Пусть |B₁| = t и

   B₁={b₁, b₂, ..., b_t}.

       По аксиоме (В.2) существует c₁ ∈ В₂ такой, что

   {с₁, b₂, ..., b_t} ∈ B.

       Аналогично, существует с₂ ∈ В₂ такой, что

   {c₁, с₂, b₃, ..., b_t} ∈ B.

       Продолжая этот процесс, получим

   {c₁, c₂, ..., c_t} ∈ B

   для некоторых с₁, с₂, ..., c_t ∈ В₂. В силу аксиомы (В.1) получаем {с₁, с₂, ..., c_t} = В₂, т.е. |B₂| ≤ t = |B_i|. Следовательно, |B₂| = |B₁|.

       Подмножество А из Е будем называть B-независимым, если оно содержится в некотором B-множестве. Ясно, что B-множества - это максимальные B-независимые множества. Обозначим через I совокупность всех B-независимых множеств.

       Заметим, что семейство I удовлетворяет аксиоме независимости (I.1). Для завершения доказательства теоремы достаточно проверить, что семейство I удовлетворяет аксиоме (I.2) и воспользоваться теоремой 1.

       Пусть I, J ∈ I и |I| < |J|. Зафиксируем базу В₂, содержащую J. Среди баз, содержащих I, выберем такую базу B₁, для которой пересечение В₁∩В₂ содержит наибольшее возможное число элементов.

       Покажем, что В₁\I ∈ В₂. Действительно, если существует b₁ ∈ В₁\I такой, что b₁ ∉ В₂, то по аксиоме (В.2) существует b₂ ∈ В₂, для которого

   B= (B₁\b₁)∪b₂ ∈ B

   и b₁ ≠ b₂, так как b₁ ∉ B₂, а b₂ ∈ B₂. Тогда |В ∩ B₂| > |B₁ ∩ B₂|, что невозможно, поскольку I ⊆ В.

       Таким образом, B₁\I, J ⊆ В₂, причем |B₁\I| +|J| = |B₁| -|I| + |J| > |B₁| = |B₂|. Следовательно, существует p ∈ (В₁\ I) ∩ J. Так как I ∪ p ∈ В₁ и p ∈ J\I, элемент p является искомым.

    Заметим, что условие (В.2) называют аксиомой Штейница о замене.

---

    Примеры.

1. Пусть Е = {v₁, ..., v_m} - некоторое множество векторов векторного пространства V над телом F. Рассмотрим множество всех максимальных линейно независимых подмножеств из Е. Оно удовлетворяет аксиомам баз (В.1) и (В.2), т.е. мы имеем матроид на Е с таким семейством баз. Этот матроид называют векторным матроидом над телом F.

2. Пусть G - произвольный ненулевой (n, m)-граф. Построим матроид циклов графа G, который будем обозначать через M(G). В качестве основного множества Е возьмем EG, в качестве баз этого матроида - остовы (точнее, каждая база - это множество всех ребер некоторого остова). Аксиома (В.1) очевидна, а аксиома (В.2) выполняется в силу леммы 4. Ясно, что в этом матроиде независимыми множествами будут ациклические множества ребер, а циклами - обычные циклы графа.

3. Пусть M(Е) - произвольный матроид на множестве Е.

       Возьмем A ⊆ Е. В качестве системы независимых множеств на A рассмотрим независимые множества исходного матроида, содержащиеся в А. Ясно, что на А мы получили матроид, который обозначают через M(А) и называют подматроидом исходного матроида.

       Пусть Е₁ - конечное множество и f - сюрьективное отображение Е₁ на Е. Определим следующим образом матроид M(Е₁) на множестве Е₁. Пусть r - ранг матроида M(Е). Семейство элементов {а₁, ..., а_r} ⊆ Е₁ назовем базой, если {f(а₁), ..., f(а_r)} - база матроида M(Е). Очевидно, аксиомы баз выполняются и мы получили матроид M(Е₁). При переходе от Е к E₁ каждый элемент a из Е мы заменяем на некоторое конечное множество элементов (составляющих полный прообраз элемента a относительно f). Для того чтобы получить произвольную базу матроида M(Е₁) мы можем поступить следующим образом: берем сначала базу b₁, ..., b_r матроида M(Е), а затем в полных прообразах элементов b₁, ..., b_r берем соответственно по одному элементу а₁, ..., а_r. Аналогично устроены и независимые множества матроида М(E₁). Можно мыслить себе, что матроид М(Е₁) получен из матроида М(Е) с помощью "размножения" элементов, т. е. заменой каждого элемента из Е на некоторое число его копий. Поэтому матроид M(Е₁) будем называть раздуванием матроида М(Е).

4. Пусть V - векторное пространство над телом F. Возьмем некоторую систему векторов v₁, ..., v_m из V (возможно с повторениями векторов). Построим матроид М, отвечающий этой системе векторов. Матроид М будет иметь m элементов. Для простоты мы можем считать, что элементами матроида М являются элементы v₁, ..., v_m, т.е. все они различны как элементы матроида М, но некоторые из них могут совпадать как элементы векторного пространства V. В качестве баз возьмем все максимальные линейно независимые подсистемы из v₁, ..., v_m. Мы получили матроид М, который, очевидно, является раздуванием некоторого векторного матроида над телом F. В дальнейшем раздувание векторного матроида над телом F также будем называть векторным матроидом над телом F.

5. Пусть

   
   

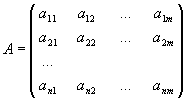
   - некоторая матрица над телом F. Строки матрицы A являются элементами пространства векторов-строк Fm. Поэтому матрице A отвечает векторный матроид над телом F, состоящий из n элементов - строк матрицы A. Этот матроид называют матроидом строк матрицы А. Отметим, что здесь строки с разными номерами являются разными элементами матроида, хотя некоторые из них могут совпадать как элементы пространства Fm. Аналогично определяется матроид столбцов матрицы А.

Теорема 12 (Ранговые аксиомы).

1. Пусть M(Е) матроид и r - его ранговая функция из P(E) в N∪{0}. Тогда для любых A, В ⊆ Е выполняется

       (r.1) 0 ≤ r(А) ≤ |А|;

       (r.2) А⊆В ∠ r(А) ≤ r(В);

       (r.3) r(А∩В) + r(A∪B) ƒ r(А) + r(В).

2. Обратно, пусть некоторая функция r из P(Е) в N∪{0} где Е - конечное непустое множество, удовлетворяет условиям (r.1), (r.2) и (r.З). Тогда она является ранговой функцией однозначно определенного матроида на Е.

Доказательство.

1. Свойства (r.1) и (r.2) очевидны. Докажем (r.З). Ясно, что A∩B ⊆ 〈A〉 ∩ 〈B〉 и A∪В ⊆ 〈А〉 ∨ 〈B〉. Используя неравенство полумодулярности, которое выполняется в решетке листов, получаем

   r(А ∩ В)+ r(A∪В) < r(〈А〉 ∩ 〈B〉) + r(〈А〉 ∨ 〈B〉) ≤ r(〈А〉) + r(〈B〉)= r(A) + r(B).

2. Обратно, пусть некоторая функция r из P(E) в N∪{0}, где Е - конечное непустое множество, удовлетворяет условиям (r.1), (r.2) и (r.З).

       Подмножество I ⊆ Е назовем r-независимым, если выполняется r(I) = |I|. Обозначим через I множество всех r-независимых подмножеств из Е. В силу (r.1) выполняется r(∅) = 0, т. е. ∅ ∈ I.

       Докажем, что семейство I удовлетворяет аксиомам независимости (1.1) и (1.2).

       Сначала проверим аксиому (I.1). Пусть I ∈ I и J ∈ I. Предположим, от противного, что r(J) < |J|. Тогда, используя (r.3) и (r.1), получаем

   |I| = r(I) = r(J∪(I \ J)) ≤ r(J) + r(I \ J) - r(∅) < |J| + (I \ J) - |I|,

   что невозможно. Следовательно, r(J) = |J|, т.е. J ∈ I.

       Прежде чем перейти к проверке аксиомы (I.2), докажем следующее вспомогательное утверждение.

       Пусть B ⊂ A ⊆ Е, r(В) = |В| и A\B = (p₁, ..., p_t). Если r(В∪p_i) = |В| для любого i = 1, ..., t, то r(А)=|В|.

       Предположим, что r(B∪p\∪ ... ∪p_j) = |В| для некоторого j = 1, ..., t-1. Тогда, применяя (r.2) и (r.З), получаем

   |B| = r(B) ≤ r(B∪p₁∪ ... ∪p_j+l) ≤ r(B∪p₁∪ ... ∪p_j) + r(B∪p_j+1) - r(B) = |B| + |B| - |B| =|B|.

       Следовательно, r(B∪p₁ ∪ ... ∪p_j+l) = |В|.

       Теперь из доказанного, очевидно, вытекает равенство r(А) = r(B∪p₁ ∪ ... ∪p_t) = |B|.

       Перейдем к проверке аксиомы (I.2). Пусть I, J ∈ I и |I| < |J|. Положим J\I = {p₁, ..., p_t}. Пусть, от противного, I∪P_i ∉ I для любого i = 1, ..., t. Тогда для i = 1, ..., t имеет место

   |I| = r(I) ≤ r(I∪p_i) < |I∪P_i| = |I| + l,

   т.е. r(I∪p_i) =|I|. Отсюда в силу доказанного нами вспомогательного утверждения получаем r(I∪J) = |I|. С другой стороны,

   |I| < |J| =r(J) ≤ r(I ∪ J),

   что противоречиво.

       Итак, мы установили справедливость для X аксиомы (1.2).

       Следовательно, семейство I является семейством независимых множеств некоторого матроида M(Е) на множестве Е.

       Осталось проверить, что исходная функция r совпадает с ранговой функцией матроида M(Е). Для этого надо показать, что для любой базы B произвольного множества А⊆Е выполняется r(А) = |В|.

       Пусть B - база множества А⊆Е. По определению 1 имеем r(В) - |В| и В - максимальное r-независимое подмножество из А. Если А = В, то равенство r(А) = |В| очевидно. Поэтому будем считать, что B ⊂ А. Пусть А\В = {p₁, ..., p_t}. В силу максимальности B для любого i = 1, ..., t множество B∪р_i не является r-независимым, т.е. r(B∪p_i) < |B∪p_i|. Тогда имеем

   |В| = r(B) ≤ r(B∪p_i) < |B∪p_i| = |B| + 1,

   т.е. r(B∪p_i) = |B| для любого i = 1, ..., t. В силу доказанного утверждения получаем r(А) = |B|.

       Теорема доказана.

Теорема 13 (Аксиомы циклов).

1. Пусть M(Е) - матроид и Ccl - семейство его циклов. Тогда

       (С.1) ∅ ∉ Ccl, если C₁, С₂ ∈ Ccl и С ≠ С₂, то С₁ ⊄ С₂ и С₂ ⊄ С₁;

       (С.2) если С₁, С₂ ∈ Ccl, С₁ ≠ С₂ и p ∈ С₁∩С₂, то существует С ∈ Ccl такой, что С ⊆ (C₁∪С₂)\p.

2. Обратно, пусть семейство C подмножеств конечного непустого множества Е удовлетворяет условиям (С.1) и (С.2), где вместо Ccl фигурирует С. Тогда семейство C совпадает с семейством циклов однозначно определенного матроида на Е.

Доказательство.

1. Свойство (С.1) очевидно вытекает из определения цикла.

       Для доказательства (С.2) достаточно проверить, что множество D = (C₁∪С₂)\p зависимо (тогда оно содержит минимальное зависимое множество - цикл). Так как D ⊆ С₁∪С₂, мы получаем

   r(D) ≤ r(C₁ ∪ С₂) ≤ r(C₁) + r(C₂) - г(C₁ ∩ С₂) =
   |С₁| - 1 + |С₂| - 1 - |C₁ ∩ С₂| =
   | C₁ ∪ С₂| - 2 < |C₁ ∪ С₂| - 1 = D

   т. e. D - зависимое множество.

2. Обратно, пусть семейство C удовлетворяет условию теоремы. Множество I ⊆ E назовем C-независимым, если оно не содержит ни одного из множеств С ∈ C. Через X обозначим семейство всех C-независимых множеств, содержащихся в Е. Проверим, что семейство С удовлетворяет аксиомам независимости (I.1) и (I.2).

       Поскольку ∅ ∉ C, имеем ∅ ∈ I и аксиома (I.1) очевидно выполняется.

       Проверим справедливость аксиомы (I.2) для семейства I. Предположим, что существуют множества I, J ∈ I такие, что |I| < |J|, для которых (I.2) неверно. Среди всех таких пар I, J выберем ту, у которой мощность |I∪J| минимальна. Положим J\I = {p₁, ..., p_t}. Если t = 1, то, очевидно, I ⊂ J и утверждение (I.2) выполняется. Поэтому имеем t ≥ 2.

       В силу нашего предположения I∪p_i ∉ I для любого i = 1, ..., t. Следовательно, существует С_i ∈ C такое, что С_i ⊆ I∪p_i, и в силу C-независимости множества I имеем p_i ∈ C_i, для любого i = 1, ..., t. Ясно, что множества С₁, ..., C_t попарно различны.

       Рассмотрим множество С₁. Для него верно р₁ ∈ С₁ ⊆ I∪p₁. В силу C-независимости J существует q₁ ∈ I\J такой, что q₁ ∈ C₁. Рассмотрим теперь множество (I\q₁)∪p₁.

       Если (I\q₁)∪p₁ ∉ X, то существует C' ∈ C, для которого p₁ ∈ C' ⊆ (I\q₁)∪p₁, и, следовательно, в силу (С.2) существует такой цикл С" ∈ C, что

   С" ⊆ (C₁ ∪ C')\p₁ ⊆ I.

       Пришли к противоречию с условием I ∈ I.

       Пусть (I\q₁) ∪ p₁ ∈ I. Заметим, что

   |((I\q₁) ∪ p₁) ∪ J| < |I ∪ J|

       Поэтому в силу выбора пары I, J, для пары (I\q₁)∪p₁, J существует элемент p_j, где j ≥ 2, такой, что

   (I\q₁) ∪ p₁ ∪ p_j ∈ I

       Возьмем множество C_j ∈ X. Для него выполняется p_j ∈ C_j ⊆ I∪p_j. Если q₁ ∉ C_j, то C_j ⊆ (I\q₁)∪р_j ⊆ (I\q₁)∪p₁∪p_j, что невозможно. Следовательно, q₁ ∈ C_j∩C_i и C_j ≠ C₁. Тогда по аксиоме (С.2) существует С ∈ C, для которого

   C ⊆ (С_j∪С₁)\q₁ ⊆ (C_j\q₁)∪(C₁\q₁) ⊆ ((I\q₁∪p_j)∪((I\q₁)∪p₁ = (I\q₁)∪p₁∪p_j ∈ I

   что невозможно.

       Итак, семейство I удовлетворяет аксиомам независимости (I.1) и (I.2). Следовательно, существует матроид M(Е) на множестве Е, для которого семейство I является семейством Ind независимых множеств. Из определения C-независимости легко следует, что семейство C совпадает с множеством Ccl циклов матроида М(Е).

    Теорема доказана.

Следствие 1.

Пусть I - произвольное независимое множество матроида M(Е) и p ∈ Е. Тогда I∪p содержит не более одного цикла.

Доказательство.

Пусть в I∪p содержится два различных цикла С₁ и С₂. Очевидно, p ∈ С₁∩ C₂ в силу независимости множества I. Тогда по аксиоме (С.2) существует цикл С такой, что

C ⊆ (C_l∪ C₂)\p ⊆ I,

что невозможно.

Следствие 2.

Для любой базы В матроида М(Е) и любого p ∈ Е\В множество B∪p содержит точно один цикл и этот цикл проходит через p.

    На следующем шаге мы рассмотрим понятие двойственного матроида.

Предыдущий шаг Содержание Следующий шаг