На этом шаге мы рассмотрим двойственный матроид.

Пусть М = M(Е) - произвольный матроид. Для X ⊆ Е через будем обозначать, как обычно, теоретико-множественное дополнение, т. е. = Е\Х. Для произвольной базы В ∈ Bs матроида М множество будем называть его кобазой. Через Bs* обозначим множество всех кобаз матроида М, т. е. Bs* = { | В ∈ Bs}.

Теорема 14.

Множество Bs* всех кобаз матроида удовлетворяет аксиомам баз (В.1) и (В.2).

Доказательство.

Поскольку для любых X, Y ∈ Е условия X ⊆ Y и X ⊇ Y эквивалентны, аксиома (В.1) очевидно выполняется.

Пусть теперь 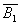и 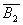- две кобазы и p ∈ . Так как р ∉ В₁, в множестве B₁∪р имеется точно один цикл С. Поскольку цикл С не лежит в B₂, существует q ∈ C ∩ . Множество (В₁∈p)\q не содержит циклов, так как мы разрушили единственный цикл, удалив элемент q. Поэтому это множество независимо и его мощность равна мощности базы В₁. Следовательно, (В₁∪p)\q - база. Тогда для соответствующей кобазы выполняется

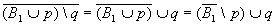где q ∈ 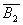. Таким образом, мы проверили аксиому Штейница о замене для кобаз.

В силу доказанной теоремы семейство кобаз Bs* задает на Е матроид, в котором исходные кобазы играют роль баз. Этот матроид называется двойственным к матроиду М и обозначается через М* = М*(Е). Конечно, (М*)* = М.

Зависимые и независимые множества, циклы матроида М* называются соответственно козависимыми и конезависимыми множествами, коциклами матроида М. Ранговая функция матроида М* называется коранговой функцией матроида М и обозначается через r*. Очевидно,

r(М) + r*(М) = |Е|.

Пусть имеется некоторое утверждение о произвольном матроиде. Если в нем заменить все используемые матроидные понятия на соответствующие копонятия и наоборот, то мы получим утверждение, которое называется двойственным к исходному утверждению. Очевидно справедлив

Принцип двойственности. Если некоторое утверждение верно для любого матроида, то двойственное к нему утверждение также верно для любого матроида.

Следующая лемма легко вытекает из определений.

Лемма 1.: Произвольное подмножество элементов матроида зависимо тогда и только тогда, когда оно имеет непустое пересечение с каждой кобазой.

В силу принципа двойственности верно следующее двойственное утверждение.

Лемма 2.

Произвольное подмножество элементов матроида козависимо тогда и только тогда, когда оно имеет непустое пересечение с каждой базой.

Лемма 3.

Для любого непустого независимого множества I ⊆ Е матроида М существует такой коцикл С*, что |I ∩ С*| = 1.

Доказательство.

Множество I можно продолжить до некоторой базы В. Возьмем p ∈ I. Тогда В∪p содержит точно один коцикл С*, для которого выполняется С*∩В = {p} = С*∩I.

Лемма 4.

Для любого цикла C и любого коцикла С* справедливо условие

|С∩С*| ≠ 1.

Доказательство.

Предположим, от противного, что C∩C* = {p}. Поскольку в силу леммы 2 коцикл C* - это минимальное подмножество из Е, имеющее непустое пересечение с каждой базой, множество C* - это максимальное подмножество из Е, не содержащее баз. Следовательно, С∪p содержит некоторую базу В. Множество С\p независимо и лежит в С*∪р. По аксиоме независимости (I.2') существует база В₁ такая, что

С\p ⊆ B₁ ⊆ C*∪p

(поскольку C*∪p содержит базу B, любое максимальное независимое подмножество из C*∪p является базой матроида). Так как C* не содержит баз, имеем p ∈ В₁. Следовательно, С ⊆ B₁ что невозможно.

Следующее утверждение нам понадобится в дальнейшем.

Теорема 15.: Подмножество X ⊆ Е является циклом матроида М тогда и только тогда, когда X есть минимальное множество среди непустых подмножеств из Е, удовлетворяющих свойству:
|Х∩С*| ≠ 1 для любого коцикла C*.
Доказательство.: Если X является циклом матроида, то в силу леммы 4 он удовлетворяет требуемому свойству, а в силу леммы 3 имеет место необходимая минимальность.
Обратно, пусть X - минимальное множество среди непустых подмножеств из Е, удовлетворяющих указанному свойству. В силу леммы 3 множество X зависимо и, следовательно, содержит некоторый цикл C. На основании леммы 4 и минимальности X получаем X = С.

Если на конечном непустом множестве Е в качестве единственной базы взять множество Е, то возникнет, очевидно, матроид, который называют свободным или дискретным матроидом на Е. Здесь Ind = P(E), r(A) = |А| (А ⊆ Е) и Ccl = ∅.

Матроид на Е₁, двойственный к свободному матроиду, называется тривиальным матроидом. Он имеет единственное независимое множество и единственную базу - пустое множество, поэтому r(А) = ∅ для любого A ⊆ Е. Его циклами являются одноэлементные подмножества из Е.

Пусть G - произвольный ненулевой (n, m, k)-граф. Рассмотрим матроид циклов М = M(G) графа G на множестве Е = ∪G. Базами этого матроида будут множества ребер графа, составляющие его остовы. Очевидно, ранг матроида r(М) = n-k есть ранг графа G, а его коранг r*(М) = m - r(М) = m - n + k совпадает с цикломатическим числом графа G.

Пусть B - некоторая база матроида М = M(G). Тогда соответствующую кобазу B называют еще и коостовом (это множество тех ребер графа, которые нужно отбросить из графа, чтобы получить его остов). В силу леммы 2 независимые множества матроида M(G) - это те и только те множества ребер графа, которые имеют непустое пересечение с каждой базой. Следовательно, козависимые множества из M(G) - это те и только те множества ребер, при стирании которых в графе G разрушаются все остовы, т. е. увеличивается число компонент связности. Таким образом, козависимые множества из M(G) - это в точности разрезающие множества ребер графа, а тогда коциклы - это разрезы! Следовательно, циклы и разрезы графа - это взаимно двойственные объекты. Матроид М*(G), двойственный к матроиду M(G), называют матроидом разрезов графа G.

Отметим, что для любого дерева Т матроид M(Т) свободен, а матроид М*(Т) тривиален.

Пример. Рассмотрим матроид циклов следующего графа:

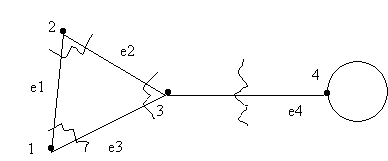
Рис.1. Пример графа

Тогда

E = {e₁, е₂, е₃, e₄, e₅} - основное множество матроида;
В₁ = {е₂, е₃, е₄}, В₂ = {е₁, е₃, е₄}, В3 = {e₁, е₂, е₄} - множество баз;
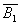= {e₁, е₅}, 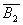= {е₂, е₅}, 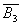= {е₃, е₅} - множество кобаз;
{e₁, e₂}, {e₁, е₃}, {е₂, е₃}, {е₄} - множество коциклов, совпадающее с множеством разрезов рассматриваемого графа.

На следующем шаге мы дадим понятие жадного алгоритма.

Предыдущий шаг Содержание Следующий шаг