На этом шаге мы рассмотрим понятие жадного алгоритма.

Пусть Е - непустое конечное множество и w - функция из Е в множество действительных чисел R. Число w(e) будем называть весом элемента e ∈ E. Для любого непустого A ⊆ E положим

и будем называть w(A) весом множества А.

Зафиксируем некоторое семейство B ⊆ I(E), в котором имеется хотя бы одно непустое множество. Будем смотреть на B как на частично упорядоченное множество относительно теоретико-множественного включения. Для удобства элементы частично упорядоченного множества I будем называть объектами.

Будем далее считать, что B удовлетворяет аксиоме независимости (I.1), т.е. подмножество объекта является объектом.

Рассмотрим следующую задачу: в частично упорядоченном множестве объектов B построить максимальный объект минимально возможного веса.

Исследуем, при каких условиях на семейство объектов следующий алгоритм решает поставленную задачу.

Жадный алгоритм.

В качестве e₁ выберем в Е элемент наименьшего возможного веса такой, что {e₁} ∈ B.
Пусть элементы e₁, ..., e_i-1 уже выбраны. В качестве е_i выберем в Е элемент наименьшего возможного веса такой, что
e_i ∉ {e₁, e₂, ..., e_i-1} и {e₁, ...,e_i} ∈ B
Выполняем 2) до тех пор, пока это возможно. Процесс обязательно завершится, и будет построен максимальный объект B = {e₁ ..., e_r) ∈ B.

Теорема 16.: Пусть семейство объектов B удовлетворяет дополнительно аксиоме независимости (I.2), т. е. B является семейством Ind всех независимых множеств некоторого нетривиального матроида на Е. Тогда любое множество B, построенное жадным алгоритмом, будет максимальным объектом минимально возможного веса.
Доказательство.: Пусть B - семейство независимых множеств некоторого нетривиального матроида М = M(Е) и объект B = {e₁, ..., e_r} построен жадным алгоритмом, как указано выше. Очевидно, B является базой матроида М.
Пусть, от противного, B не является базой минимального возможного веса. Среди баз минимального возможного веса выберем базу B', для которой число |B∩B'| имеет наибольшее возможное значение. Так как B ≠ B', имеем В ⊄ В'. Возьмем элемент e_i с наименьшим номером такой, что e_i ∉ B'. Тогда {e₁, ..., e_i-1} ⊆ B∩B'. Множество В'∪е_i содержит точно один цикл C. Поскольку C ⊄ В, существует e ∈ С\В. Положим В" = (В'∪e_i)\e. Отбросив e, мы разрушили единственный цикл в B'∪e_i. Следовательно, B" - независимое множество матроида М и |В"| = |В'|, т.е. В" - база матроида М. Кроме того, очевидно, |В" ∩ В| > |В' ∩ В|. Поэтому w(B") > w(B') в силу выбора базы В'. Так как w(B") = w(В') + w(e_i) - w(e) получаем w(e_i) - w(e) > 0, т.е. w(e_i) > w(e). Последнее неравенство противоречит тому, что на i-м шаге жадного алгоритма был выбран элемент e_i, а не элемент e, хотя в ∉ {e₁, ..., e_i-1} ⊆ В и множество {e₁, ..., e_i-1, e} ⊆ В' независимо.

Пусть G - связный неодноэлементный граф. Рассмотрим на множестве его ребер Е = E(G) некоторую весовую функцию w, которая каждому ребру e ставит в соответствие вес ребра w(e) ∈ R. Семейство G ациклических наборов ребер является семейством независимых множеств матроида циклов M(G) графа G. Базами этого матроида являются, по существу, остовы графа G. В силу доказанной теоремы жадный алгоритм в данном случае строит остов минимально возможного веса в графе G.

Следующее предложение показывает, что выполнение аксиомы независимости (I.2) необходимо для того, чтобы при любой весовой функции жадный алгоритм всегда строил бы в семействе объектов I максимальный объект минимально возможного веса.

Предложение 1.: Пусть семейство объектов I не удовлетворяет аксиоме независимости (I.2). Тогда существует весовая функция w из E в R, для которой любое применение жадного алгоритма строит в I максимальный объект, не являющийся максимальным объектом минимально возможного веса.
Доказательство.: Пусть семейство объектов I не удовлетворяет аксиоме независимости (I.2). Тогда существуют I, J ∈ I такие, что t = |I| < |J| = t + 1, где е ∈ N, и I ∪ p ∉ I для любого p ∈ J\I. Пусть |I∩J| = s, где s ∈ N∪0. Очевидно s < t.

В качестве весовой функции рассмотрим следующую функцию

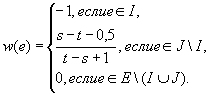
При такой весовой функции w жадный алгоритм сначала обязательно выберет все элементы множества I, а затем (возможно) выберет элементы из Е\(I∪J) и построит некоторое максимальное множество I₁ такое, что I ⊆ I₁ и w(I₁) = w(I) = -t.

Заметим, далее, что

Расширим J до некоторого максимального в I множества J₁. Тогда, очевидно, w(J₁) ≤ w(J) < w(I₁).

Следовательно, любое построенное жадным алгоритмом максимальное множество I₁ не является максимальным объектом минимально возможного веса.

На следующем шаге мы рассмотрим теорему Радо - Эдмондса.

Предыдущий шаг Содержание Следующий шаг