На этом шаге мы рассмотрим уточнения теоремы Шеннона.

Перечислим ограничения, не учитываемые теоремой Шеннона.

Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы. Это не должно восприниматься как заметное ограничение, поскольку действие большинства практических устройств связи основано именно на этих процессах.
Любое подобное устройство использует не весь спектр частот колебаний, а лишь какую-то его часть; например, в телефонных линиях используются колебания с частотами от 300 Гц до 3400 Гц. Согласно теореме отсчетов определяющим является значение верхней границы частоты – обозначим его .

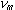Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:

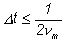(1)

Можно перефразировать теорему отсчетов:

Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать t, определяемый в соответствии с (1).

Например, для точной передачи речевого сигнала с частотой до = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.

Однако, помимо временной развертки, дискретизация имеет и другую составляющую – квантование. Какими соображениями определяется шаг квантования Z? Любой получатель сообщения – человек или устройство – всегда имеют конечную предельную точность распознавания величины сигнала. Например, человеческий глаз в состоянии различить около 16 миллионов цветовых оттенков; это означает, что при квантовании цвета нет смысла делать большее число градаций. При передаче речи достаточной оказывается гораздо меньшая точность – около 1%; следовательно, для амплитуды звуковых колебаний Z 0,01·Z^max, а алфавит для обозначения всех градаций громкости должен содержать 100 знаков. Мы приходим к заключению, что шаг квантования определяется чувствительностью приемного устройства.

Указанные соображения по выбору шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель. Термины "цифровая запись", "цифровой сигнал" следует понимать как дискретное представление с применением двоичного цифрового алфавита.

Таким образом, преобразование сигналов типа ND, как и обратное DN, может осуществляться без потери содержащейся в них информации.

Преобразование типа D₁D₂ состоит в переходе при представлении сигналов от одного алфавита к другому – такая операция носит название перекодировка и может осуществляться без потерь. Примерами ситуаций, в которых осуществляются подобные преобразования, могут быть: запись-считывание с компьютерных носителей информации; шифровка и дешифровка текста; вычисления на калькуляторе.

Таким образом, за исключением N₁N₂ в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях ND и DN обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другими ее достоинствам следует отнести:

высокая помехоустойчивость;
простота и, как следствие, надежность и относительная дешевизна устройств по обработке информации;
точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;
универсальность устройств.

Последнее качество – универсальность – оказывается следствием того обстоятельства, что любые дискретные сообщения, составленные в различных алфавитах, посредством обратимого кодирования можно привести к единому алфавиту. Это позволяет выделить некоторый алфавит в качестве базового (из соображений удобства, простоты, компактности или каких-либо иных) и представлять в нем любую дискретную информацию. Тогда устройство, работающее с информацией в базовом алфавите, оказывается универсальным в том отношении, что оно может быть использовано для переработки любой иной исходной дискретной информации. Таким базовым алфавитом, как мы увидим в дальнейшем, является двоичный алфавит, а использующим его универсальным устройством – компьютер.

Несимметричность непрерывной и дискретной информации имеет более глубокую основу, чем просто особенности представляющих сигналов. Дело в том, что информация, порождаемая и существующая в природе, связана с материальным миром – это размеры, форма, цвет и другие физические, химические и прочие характеристики и свойства объектов. Данная информация передается, как было сказано, посредством физических и иных взаимодействий и процессов. Бессмысленно ставить вопросы: для чего существует такая информация и кому она полезна? Эту природную информацию можно считать хаотической и неупорядоченной, поскольку никем и ничем не регулируется ее появление, существование, использование. Чаще всего она непрерывна по форме представления. Напротив, дискретная информация – это информация, прошедшая обработку – отбор, упорядочение, преобразование; она предназначена для дальнейшего применения человеком или техническим устройством. Дискретная информация даже может не иметь прямого отношения к природе и материальным объектам, например представления и законы математики. Другими словами, дискретная – это уже частично осмысленная информация, т.е. имеющая для кого-то смысл и значение и, как следствие, более высокий (с точки зрения пользы) статус, нежели непрерывная, хаотичная. Однако в информатике, как было сказано, этот смысл не отслеживается, хотя и подразумевается. Эту же мысль можно выразить иначе: информатика имеет дело не с любой информацией и не с информацией вообще, а лишь с той, которая кому-то необходима; при этом не ставятся и не обсуждаются вопросы "Зачем она нужна?" и "Почему именно эта?" – это определяет потребитель информации.

Отсюда становится понятной приоритетность дискретной формы представления информации по отношению к непрерывной в решении глобальной задачи автоматизации обработки информации. Приведенные в данном параграфе соображения позволяют нам в дальнейшем исследовать только дискретную информацию, а для ее представления (фиксации) использовать некоторый алфавит. При этом нет необходимости рассматривать физические особенности передачи и представления, т.е. характер процессов и виды сигналов, – полученные результаты будут справедливы для любой дискретной информации независимо от реализации сообщения, с которым она связана. С этого момента и начинается наука информатика.

Предыдущий шаг Содержание