На этом шаге мы рассмотрим построение функции сложности по упрваляющему графу.

Рассмотрим возможные варианты.

Управляющий граф представляет собой линейный участок. Сложность равна сумме весов вершин, принадлежащих линейному участку, и является константой, если на участке нет вершин - вызовов процедур. Если такие вершины есть, то их вес равен функциям сложности соответствующих процедур.
Управляющий граф содержит разветвления, но не содержит циклов. Это означает, что вычислительный процесс в зависимости от исходных данных может направиться по одной из конечного числа ветвей, начинающихся в начальной вершине и заканчивающихся в одной из конечных вершин. Расчет функции сложности зависит от того, рассматривается худший случай или средний случай.
Управляющий граф содержит цикл, порожденный оператором for. Если выражения, определяющие начальное и конечное значения параметра цикла суть константы, то нетрудно подсчитать, сколько раз будет выполняться тело цикла и умножить на этот коэффициент вес тела цикла. Если выражения зависят от исходных данных, то можно оценить значение разности этих выражений в худшем или среднем случаях.
Управляющий граф содержит цикл, порожденный операторами while или repeat. Циклы while и repeat могут вызвать больше затруднений при анализе, чем оператор for, так как количество исполнений тела цикла зависит от истинности или ложности условия, а переменные, входящие в состав условия изменяются в теле цикла, причем оценить величину и направленность этого изменения достаточно сложно.

Управляющий граф содержит разветвления

Для худшего случая нужно вычислить вес каждой ветви как сумму весов входящих в нее вершин, после чего найти максимальный из весов ветвей. Это и будет сложностью процедуры.

Пример 1. Управляющий граф содержит 10 вершин с весом {3, 5, 1,4, 3, 4, 6, 8, 5, 3}. Вершина 3 (вес равен 1) соответствует вычислению условия в операторе if; вершины 4, 5, 6 входят в часть then, вершины 7, 8 входят в часть else. Таким образом, имеется две ветви с весом 3+5+1+4+3+4+5+3 = 28 и 3+5+1+6+8+5+3 = 31; сложность равна 31.

Пример 2. Тот же граф, что и в примере 1, но вершина 8 соответствует вызову процедуры, имеющей сложность 2V + 1. В этом случае функция сложности равна max (28, 2V+24 ) = 24+max(4, 2V) = 24 + 2 max ( 2, V ).

Для среднего случая, кроме веса ветвей, нужно оценить еще и частоты ветвей. Под частотой ветви понимается отношение числа выполнений программы, при которых исполнялись операторы, принадлежащие данной ветви, к общему числу выполнений программы. Тогда сложность программы будет вычисляться как сумма произведений весов ветвей на их частоты. Если все комбинации исходных данных программы равновероятны, то частоты ветвей можно оценить следующим образом.

Пусть управляющий граф содержит разветвления с условиями C₁, C₂, C₃, ..., C_n, причем проверка условия C₁ производится всегда первой по ходу выполнения программы. Следовательно, условие С₁ разбивает все ветви на две группы: для ветвей первой группы это условие истинно, а для ветвей второй группы - ложно. Условие С₂ разбивает группу ветвей с истинным условием С₁ на две группы, удовлетворяющие условиям C₁ and C₂ и C₁ and not С₂. Условие С₃ порождает группы ветвей, удовлетворяющих условиям not C₁ and С₃ и not C₁ and not С₃ и т. д.

Множество D комбинаций исходных данных также делится на две части D1 и D2 и это деление порождается условием C₁ даже, если сами исходные данные не входят в формулировку условия, а входят только константы и промежуточные переменные. В свою очередь, D1 делится на подмножества D2 и D3 в соответствии с условием C₂ и так далее. На рисунке 1 изображены примеры управляющего графа программы и разбиений областей D. Три условных оператора изображены черными вершинами, область D делится сначала сплошной линией на подобласти D1 и D2, а затем каждая из них делится пунктирными линиями на подобласти D3, D4 и D5, D6.

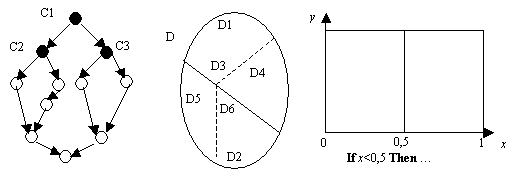
Рис.1. Управляющий граф и разбиение области данных

Каждая подобласть, не разделенная на более мелкие части, соответствует одной ветви в управляющем графе. Обозначим все такие области d_i. Тогда, считая все комбинации исходных данных равновероятными, можем оценить частоту исполнения i-й ветви как отношение мощности множества d_i к мощности множества D, p_i = |d_i|/|D|. Если i-я ветвь имеет вес l_i то сложность программы можно оценить величиной

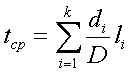
где k - количество ветвей.

Пример 3. Тот же граф, что и в примере 1. Условие в операторе if имеет вид (x<0,5), где x - входная переменная, значения которой принадлежат интервалу [0,1]. Если более подробной информации о входной переменной нет, то можно предполагать, что вероятность получить на входе значение x ∈ [0, 0,5] равна вероятности получить x ∈ [0,5, 1] и, значит та и другая вероятности равны 0,5. Следовательно, и вероятности ветвей одинаковы; средняя сложность равна 28(1/2) + 31(1/2) = 29,5 .

Пример 4 (объединение условий примеров 2 и 3). Средняя сложность равна 28(1/2) + (2V + 24)(1/2) = V + 26.

На следующем шаге мы продолжим рассматривать построение функции сложности по управляющему графу.

Предыдущий шаг Содержание Следующий шаг