На этом шаге мы рассмотрим построение функции сложности по управляющему графу, содержащему цикл for.

Управляющий граф содержит цикл, порожденный оператором for

    Если выражения, определяющие начальное и конечное значения параметра цикла - константы, то подсчитываем, сколько раз будет выполняться тело цикла и умножаем на этот коэффициент вес тела цикла. Если выражения зависят от исходных данных, то оцениваем значение разности этих выражений в худшем или среднем случаях.

  for i := 1 to x do 
    <тело цикла>, 

где x - входная переменная, x∈[1, 100]. Тело цикла выполняется x раз, худший случай реализуется при x =100. Если предположить равновероятность различных значений x, то среднее количество выполнений тела цикла равно (1/100)(1+2+3+ ...+100) = 50,5.

  for i := 1 to x do 
     for j := i to x do 
       <тело цикла>;

входная переменная x∈[1, 5]. Тело цикла выполняется x + (x-1)+(х-2)+ ...+ 1 = x (х+1)/2 раз. Верхняя граница сложности = max = (x (х+1)/2) = 13. Среднее значение сложности подсчитать несколько труднее. Снова положим, что все 5 возможных значений x равновероятны. Тогда среднее значение сложности равно:

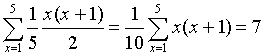
    Проведем анализ итеративного алгоритма. Процедура MULTIPLY перемножает две квадратные n*n матрицы А = {a_ij} и B = {b_ij}, получая матрицу C = {c_ij}.

procedure MULTIPLY (n: integer; a, b: matrix; var c: matrix);
var 
   i, j, k: integer;
begin 
  for i := 1 to n do  {Цикл 1.}
    for j := 1 to n do  {Цикл 2 и начало тела цикла 1.}
      begin
         c[i, j] := 0; {Начало тела цикла 2.} 
         for k := 1 to n do    {Цикл 3.}
            c[i, j] := c[i, j] + a[i, k] * b[k, j]; {Тело цикла 3.} 
      end {Конец тела цикла 2; конец тела цикла 1.}
end

    Тип данных matrix определен вне процедуры как двумерный массив. Время доступа к элементам массивов и другие скрытые операции учитываться не будут. Прежде всего выберем параметр V. Простой анализ текста показывает, что за параметр сложности данных можно взять размер n матриц, участвующих в вычислениях. Поскольку процедура представляет собой цикл по переменной i, то ее временная сложность

  Тα (n) = n*(сложность тела цикла 1).

    В свою очередь,

  сложность тела цикла l = n*(сложность тела цикла 2) 

и, следовательно,

  Тα(n) = n * ( n * (сложность тела цикла 2)).

    Тело цикла 2 состоит из одного оператора присваивания и цикла 3. Таким образом,

  Тα(n) = n * ( n * (1 + n * (сложность тела цикла 3))).

    Тело внутреннего цикла включает умножение, сложение и присваивание (3 операции). Окончательно получаем

  Тα(n) = n * (n * (1 + a * 3)) = 3n3 + n2

    Здесь управляющий граф не строили, так как структура текста процедуры достаточно прозрачна. Результат является одновременно и верхней границей и средней оценкой в силу того, что размер матриц однозначно определяет объем работы.

    Следует отметить также, что фактически был проведен рекурсивный процесс оценки функции сложности.

    На следующем шаге мы закончим рассматривать построение функции сложности по управляющему графу.

Предыдущий шаг Содержание Следующий шаг